题目内容
1.已知函数y=$\frac{1}{3}$x2,y=$\frac{1}{3}$(x+3)2和y=$\frac{1}{3}$(x-3)2(1)在同一直角坐标系中画出它们的图象;
(2)分别说出各个函数图象的开口方向、对称轴和顶点坐标;
(3)讨论各个函数的性质.
分析 (1)利用描点法可画出这三个函数的图象;
(2)分别由图象可得出开口方向、对称轴及顶点坐标.
(3)根据二次函数的对称轴和开口方向确定其增减性即可.
解答 解:(1)三个函数的图象如图所示: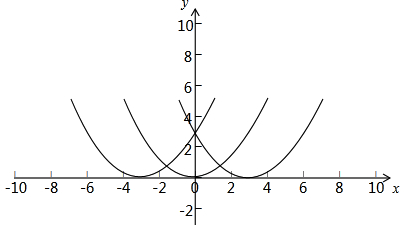
(2)由图象可知函数y=$\frac{1}{3}$x2开口向上,对称轴为x=0,顶点坐标为(0,0);
函数y=$\frac{1}{3}$(x+3)2开口向上,对称轴为x=-3,顶点坐标为(-3,0);
函数y=$\frac{1}{3}$(x-3)2开口向上,对称轴为x=3,顶点坐标为(3,0).
(3)y=$\frac{1}{3}$x2当x<0时y随着x的增大而减小,当x>0时y随着x的增大而增大;
y=$\frac{1}{3}$(x+3)2当x<-3时y随着x的增大而减小,当x>-3时y随着x的增大而增大;
y=$\frac{1}{3}$(x-3)2当x<3时y随着x的增大而减小,当x>3时y随着x的增大而增大.
点评 本题考查了二次函数的图象和性质,解题的关键是能够正确的作出二次函数的图象,掌握函数的性质.

练习册系列答案
相关题目