题目内容
某报社为了解苏州市民对大范围雾霾天气的成因、影响以及应对措施的看法,做了一次抽样调查,调查结果共分为四个等级:A.非常了解;B.比较了解;C.基本了解;D.不了解.根据调查统计结果,绘制了不完整的三种统计图表.请结合统计图表,回答下列问题.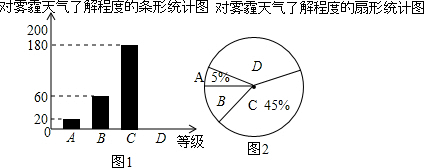
(1)本次参与调查的市民共有 人,m= ,n= ;
(2)图2所示的扇形统计图中D部分扇形所对应的圆心角是 度;
(3)请将图1的条形统计图补充完整;
(4)根据调查结果.学校准备开展关于雾霾知识竞赛,某班要从小明和小刚中选一人参加,现设计了如下游戏来确定:在一个不透明的袋中装有2个红球和3个白球,它们除了颜色外都相同,小明先从袋中随机摸出一个球,小刚再从剩下的四个球中随机摸出一个球,若摸出的两个球颜色相同,则小明去;否则小刚去.现在,小明同学摸出了一个白球,则小明参加竞赛的概率为多少?

| 对雾霾的了解程度 | 百分比 |
| A非常了解 | 5% |
| B比较了解 | m |
| C基本了解 | 45% |
| D不了解 | n |
(2)图2所示的扇形统计图中D部分扇形所对应的圆心角是
(3)请将图1的条形统计图补充完整;
(4)根据调查结果.学校准备开展关于雾霾知识竞赛,某班要从小明和小刚中选一人参加,现设计了如下游戏来确定:在一个不透明的袋中装有2个红球和3个白球,它们除了颜色外都相同,小明先从袋中随机摸出一个球,小刚再从剩下的四个球中随机摸出一个球,若摸出的两个球颜色相同,则小明去;否则小刚去.现在,小明同学摸出了一个白球,则小明参加竞赛的概率为多少?
考点:条形统计图,扇形统计图,列表法与树状图法
专题:
分析:(1)利用本次参与调查的市民人数=A等级的人数÷对应的百分比.m=
,n=1-A,B,C等级的人数求解.
(2)利用扇形统计图中D部分扇形所对应的圆心角=360°×D类的百分比.
(3)D部分的人数=总人数×D部分的百分比.再画图.
(4)根据小刚摸出白球和红球的概率,即可得出小明参加竞赛的概率.
| B等级的人数 |
| 总人数 |
(2)利用扇形统计图中D部分扇形所对应的圆心角=360°×D类的百分比.
(3)D部分的人数=总人数×D部分的百分比.再画图.
(4)根据小刚摸出白球和红球的概率,即可得出小明参加竞赛的概率.
解答:解:(1)本次参与调查的市民共有20÷5%=400(人),
m=
=15%,n=1-5%-45%-15%=35%.
故答案为:400,15%,35%.
(2)扇形统计图中D部分扇形所对应的圆心角是360°×35%=126°.
故答案为:126.
(3)D部分的人数为:400×35%=140(人).
如图1,

(4)∵小明同学摸出了一个白球,
∴里面还有2个红球和2个白球,
∴小刚再从剩下的四个球中随机摸出一个球,白球和红球的概率是
,
∴小明参加竞赛的概率为
.
m=
| 60 |
| 400 |
故答案为:400,15%,35%.
(2)扇形统计图中D部分扇形所对应的圆心角是360°×35%=126°.
故答案为:126.
(3)D部分的人数为:400×35%=140(人).
如图1,

(4)∵小明同学摸出了一个白球,
∴里面还有2个红球和2个白球,
∴小刚再从剩下的四个球中随机摸出一个球,白球和红球的概率是
| 1 |
| 2 |
∴小明参加竞赛的概率为
| 1 |
| 2 |
点评:此题考查了条形统计图,扇形统计图,列表法与树状图法,弄清题意是解本题的关键.

练习册系列答案
 全优考典单元检测卷及归类总复习系列答案
全优考典单元检测卷及归类总复习系列答案
相关题目
若a是有理数,则下列说法正确的是( )
| A、|a|一定是正数 |
| B、|-a|一定是正数 |
| C、-|-a|一定是负数 |
| D、|a|+1一定是正数 |
下列运算正确的是( )
| A、-24=16 | ||
| B、-(-2)=2 | ||
C、(-
| ||
| D、(-2)3=8 |