题目内容
10.根据相应自变量的取值范围,求下列函数的最大值或最小值.(1)y=-x2-2x(-3<x<2);
(2)y=2x2-2x+1(-1≤x≤1).
分析 (1)利用配方法将已知函数方程转化为顶点式,然后根据抛物线的性质求最值;
(2)利用配方法将已知函数方程转化为顶点式,然后根据抛物线的性质求最值;
解答 解:(1)y=-x2-2x=-(x+1)2+1,则该抛物线的顶点坐标是(-1,1).
∵-3<x<2,该抛物线的开口方向向下,
∴当x=-1时,该函数的最大值是1;
(2)y=2x2-2x+1=2(x-$\frac{1}{2}$)2-$\frac{1}{2}$,则该抛物线的顶点坐标是($\frac{1}{2}$,-$\frac{1}{2}$).
∵-1≤x≤1,该抛物线的开口方向向上,
∴当x=$\frac{1}{2}$时,该函数的最小值是-$\frac{1}{2}$.
点评 本题考查了二次函数的最值.求二次函数的最大(小)值有三种方法,第一种可由图象直接得出,第二种是配方法,第三种是公式法.

练习册系列答案
相关题目
18.计算($\sqrt{2}$+1)2016•($\sqrt{2}$-1)2015的结果是( )
| A. | 1 | B. | -1 | C. | $\sqrt{2}$+1 | D. | $\sqrt{2}$-1 |
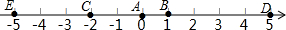 如图,A点的初始位置位于数轴上的原点,现对A点做如下移动:第1次从原点向右移动1个单位长度至B点,第2次从B点向左移动3个单位长度至C点,第3次从C点向右移动6个单位长度至D点,第4次从D点向左移动9个单位长度至E点,…,依此类推,这样至少移动1001次后该点到原点的距离不小于1499.
如图,A点的初始位置位于数轴上的原点,现对A点做如下移动:第1次从原点向右移动1个单位长度至B点,第2次从B点向左移动3个单位长度至C点,第3次从C点向右移动6个单位长度至D点,第4次从D点向左移动9个单位长度至E点,…,依此类推,这样至少移动1001次后该点到原点的距离不小于1499.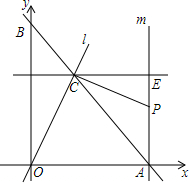 如图,直线y=-x+$\sqrt{2}$分别交x轴、y轴于A、B两点,经过点A的直线m⊥x轴,直线l经过原点O交线段AB于点C,过点C作OC的垂线,与直线m相交于点P,现将直线l绕O点旋转,使交点C在线段AB上由点B向点A方向运动.
如图,直线y=-x+$\sqrt{2}$分别交x轴、y轴于A、B两点,经过点A的直线m⊥x轴,直线l经过原点O交线段AB于点C,过点C作OC的垂线,与直线m相交于点P,现将直线l绕O点旋转,使交点C在线段AB上由点B向点A方向运动.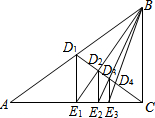 如图,已知Rt△ABC,D1是斜边AB的中点,过D1作D1E1⊥AC于E1,连结BE1交CD1于D2;过D2作D2E2⊥AC于E2,连结BE2交CD1于D3;过D3作D3E3⊥AC于E3,…,如此继续,可以依次得到点D4,D5,…,Dn,分别记△BD1E1,△BD2E2,△BD3E3,…,△BDnEn的面积为S1,S2,S3,…Sn.若S△ABC=1,则S2010=$\frac{1}{201{1}^{2}}$.
如图,已知Rt△ABC,D1是斜边AB的中点,过D1作D1E1⊥AC于E1,连结BE1交CD1于D2;过D2作D2E2⊥AC于E2,连结BE2交CD1于D3;过D3作D3E3⊥AC于E3,…,如此继续,可以依次得到点D4,D5,…,Dn,分别记△BD1E1,△BD2E2,△BD3E3,…,△BDnEn的面积为S1,S2,S3,…Sn.若S△ABC=1,则S2010=$\frac{1}{201{1}^{2}}$.