题目内容
20. 已知:PD与⊙O相切于点A,点O在∠DPE的平分线上,求证:PE是⊙O的切线.
已知:PD与⊙O相切于点A,点O在∠DPE的平分线上,求证:PE是⊙O的切线.
分析 连接OA,作OM⊥PE于M,由切线的性质定理得出OA⊥PD,由角平分线的性质定理得出OM=OA,即可得出结论.
解答 证明:连接OA,作OM⊥PE于M,如图所示:
∵PD与⊙O相切于点A,
∴OA⊥PD,
∵点O在∠DPE的平分线上,
∴OM=OA,
又∵OM⊥PE,
∴PE是⊙O的切线.
点评 本题考查了切线的判定与性质、角平分线的性质定理;熟练掌握切线的性质,通过作辅助线证明OM=OA是解决问题的关键.

练习册系列答案
 天天向上口算本系列答案
天天向上口算本系列答案
相关题目
5. 如图,△ABC≌△EFD,AB∥EF,DF∥BC,则∠B的对应角是( )
如图,△ABC≌△EFD,AB∥EF,DF∥BC,则∠B的对应角是( )
 如图,△ABC≌△EFD,AB∥EF,DF∥BC,则∠B的对应角是( )
如图,△ABC≌△EFD,AB∥EF,DF∥BC,则∠B的对应角是( )| A. | ∠F | B. | ∠FDE | C. | ∠E | D. | 以上都不正确 |
9.在同一平面坐标系中,抛物线y=-x2+2x-3通过平移得到的抛物线为y=-x2-4x+1,下面对抛物线y=-x2+2x-3平移得到的抛物线y=-x2-4x+1的描述正确的是( )
| A. | 向右平移3个单位,再向上平移7个单位 | |
| B. | 向左平移3个单位,再向上平移7个单位 | |
| C. | 向右平移3个单位,再向下平移7个单位 | |
| D. | 向左平移3个单位,再向下平移7个单位 |
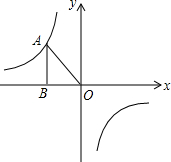 已知如图,反比例函数y=-$\frac{6}{x}$的图象上有一点A(-2,■),它的纵坐标被墨水污染了,根据题意,解答下列问题.
已知如图,反比例函数y=-$\frac{6}{x}$的图象上有一点A(-2,■),它的纵坐标被墨水污染了,根据题意,解答下列问题.