题目内容
 如图,大正方形中有两个小正方形,分别用S1,S2表示两个小正方形的面积,那么以下对S1,S2的大小关系判断正确的是
如图,大正方形中有两个小正方形,分别用S1,S2表示两个小正方形的面积,那么以下对S1,S2的大小关系判断正确的是
- A.S1>S2
- B.S1=S2
- C.S1<S2
- D.无法确定
A
分析:设大正方形的边长是2,则面积是S1的小正方形的边长是1,则面积是1,利用相似三角形的对应边的高的比等于相似比即可求得面积是S2的正方形的边长,从而求得面积,进而可以比较.
解答:设大正方形的边长是2,则面积是S1的小正方形的边长是1,则S1=1,对角线长是2 ;
;
 作CN⊥BC于点N,交DE与点M.
作CN⊥BC于点N,交DE与点M.
∵DE∥AB,
∴△CED∽△CAB,
∴ =
=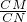 ,
,
又CN= AB=
AB= ,设面积是S2的正方形的边长是a,则
,设面积是S2的正方形的边长是a,则 =
= ,
,
解得:a= .
.
则S2=( )2=
)2= .
.
则S1>S2.
故选A.
点评:本题考查了相似三角形的性质:相似三角形的对应边的高的比等于相似比,利用性质求得面积是S2的正方形的边长是关键.
分析:设大正方形的边长是2,则面积是S1的小正方形的边长是1,则面积是1,利用相似三角形的对应边的高的比等于相似比即可求得面积是S2的正方形的边长,从而求得面积,进而可以比较.
解答:设大正方形的边长是2,则面积是S1的小正方形的边长是1,则S1=1,对角线长是2
 ;
; 作CN⊥BC于点N,交DE与点M.
作CN⊥BC于点N,交DE与点M.∵DE∥AB,
∴△CED∽△CAB,
∴
 =
=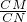 ,
,又CN=
 AB=
AB= ,设面积是S2的正方形的边长是a,则
,设面积是S2的正方形的边长是a,则 =
= ,
,解得:a=
 .
.则S2=(
 )2=
)2= .
.则S1>S2.
故选A.
点评:本题考查了相似三角形的性质:相似三角形的对应边的高的比等于相似比,利用性质求得面积是S2的正方形的边长是关键.

练习册系列答案
相关题目
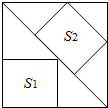 如图,边长为6的大正方形中有两个小正方形,若两个小正方形的面积分别为S1,S2,则S1+S2的值为( )
如图,边长为6的大正方形中有两个小正方形,若两个小正方形的面积分别为S1,S2,则S1+S2的值为( )| A、16 | B、17 | C、18 | D、19 |
 如图所示,在一个大正方形中有两个小正方形,它们的面积分别为m、n,则
如图所示,在一个大正方形中有两个小正方形,它们的面积分别为m、n,则 如图,大正方形中有两个小正方形,分别用S1,S2表示两个小正方形的面积,那么以下对S1,S2的大小关系判断正确的是( )
如图,大正方形中有两个小正方形,分别用S1,S2表示两个小正方形的面积,那么以下对S1,S2的大小关系判断正确的是( ) 如图:边长为12的大正方形中有两个小正方形,若两个小正方形的面积分别为S1、S2,则S1+S2的值为( )
如图:边长为12的大正方形中有两个小正方形,若两个小正方形的面积分别为S1、S2,则S1+S2的值为( )