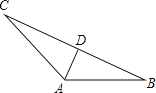
[题目]如图.在△ABC中.∠CAB=120°.AD是∠CAB的平分线.AC=10.AB=8．(1)求,(2)求AD的长．题目和参考答案——青夏教育精英家教网—

题目内容

【题目】如图，在△ABC中，∠CAB=120°，AD是∠CAB的平分线，AC=10，AB=8．

（1）求；（2）求AD的长．

【答案】（1）；（2）.

【解析】试题分析：(1)、过点C作CE∥AB，交AD的延长线于E，根据角平分线以及平行线的性质得出△ACE为等边三角形，根据平行得出△CDE∽△BDA，即，从而得出答案；(2)、根据三角形相似得出，从而求出AD的长度．

试题解析：解：（1）过点C作CE∥AB，交AD的延长线于E，

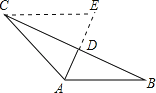
∵AD平分∠CAB，∠CAB=120°， ∴∠CAD=∠BAD=60°．

∵CE∥AB， ∴∠E=∠BAD=60°， ∴△ACE是等边三角形， ∴CE=AC=10．

又∵CE∥AB， ∴△CDE∽△BDA， ∴==

（2）由（1）知，△ACE是等边三角形， ∴AE=10． ∵CE∥AB，

∴ ∴AD=．

练习册系列答案

相关题目

【题目】如图,在平面直角坐标系中,A(a，0)，B（b，0），C(-1，2)，且+(a+2b-4)2=0.

（1）求a，b的值.

（2）在y轴的正半轴上存在一点M，使S△COM=S△ABC，求出点M的坐标.

（3）在坐标轴的其他位置是否有在点M，使S△COM=S△ABC仍成立？若存在，请直接写出符合条件的点M的坐标.

【题目】为切实做好校园疫情防控和开学的各项准备工作，某校准备再次购进免手洗消毒凝胶和医用口罩用于防疫，若购进30箱医用口罩和20箱免手洗消毒凝胶共需8500元；若购进40箱医用口罩和10箱免手洗消毒凝胶共需8000元．

（1）求医用口罩和免手洗消毒凝胶每箱购进价格分别为多少元？

（2）若该校购进免手洗消毒凝胶的数量比购进医用口罩数量的2倍少10箱，且用于购置两种物资的总经费不超过9000元，则该校至多购进医用口罩多少箱？

【题目】如图，对称轴为直线x=的抛物线与y轴交于点C（0，﹣3），与x轴交于A、B两点（点A在点B的左侧），AB=5

（1）求A、B两点的坐标及该抛物线对应的解析式；

（2）D为BC的中点，延长OD与抛物线在第四象限内交于点E，连结AE、BE．

①求点E的坐标；

②判断ABE的形状，并说明理由；

（3）在x轴下方的抛物线上，是否存在一点P，使得四边形OBEP是平行四边形？若存在，求出点P的坐标；若不存在，请说明理由．

【题目】为了解九年级学生的体能情况，学校组织了一次体能测试，并随机选取50名学生的成绩进行统计，得出相关统计表和统计图(其中部分数据不慎丢失，暂用字母m，n表示).

成绩等级	优秀	良好	合格	不合格
人数	m	30	n	5

请根据图表所提供的信息回答下列问题：

(1)统计表中的m＝，n＝；并补全频数分布直方图；

(2)若该校九年级有500名学生，请据此估计该校九年级学生体能良好及良好以上的学生有多少人？

【题目】为推广阳光体育“大课间”活动，我市某中学决定在学生中开设A：实心球，B：立定跳远，C：跳绳，D：跑步四种活动项目．为了了解学生对四种项目的喜欢情况，随机抽取了部分学生进行调查，并将调查结果绘制成如图①②的统计图．请结合图中的信息解答下列问题：

（1）在这项调查中，共调查了多少名学生？

（2）请计算本项调查中喜欢“立定跳远”的学生人数和所占百分比，并将两个统计图补充完整；

（3）若调查到喜欢“跳绳”的5名学生中有3名男生，2名女生．现从这5名学生中任意抽取2名学生．请用画树状图或列表的方法，求出刚好抽到同性别学生的概率．

【题目】如图，在△ABC中，∠C＝90°，D是BC边上一点，以DB为直径的⊙O经过AB的中点E，交AD的延长线于点F，连接EF.

(1)求证：∠1＝∠F；

(2)若sinB＝，EF＝2，求CD的长．

【题目】如图，已知直线l1∥l2，直线l3和直线l1、l2交于点C和D，在直线l3上有点P（点P与点C、D不重合），点A在直线l1上，点B在直线l2上。

（1）如果点P在C、D之间运动时，试说明∠1+∠3=∠2；

（2）如果点P在直线l1的上方运动时，试探索∠1，∠2，∠3之间的关系又是如何？

（3）如果点P在直线l2的下方运动时，试探索∠PAC，∠PBD，∠APB之间的关系又是如何？（直接写出结论）

【题目】如图，已知A（，y1），B（2，y2）为反比例函数y=图象上的两点，动点P（x，0）在x轴正半轴上运动，当线段AP与线段BP之差达到最大时，点P的坐标是_____．

试题分类