题目内容
函数y=x2-3x-4的图象开口分析:由y=x2-3x-4配方,将一般式转化为顶点式,可确定抛物线的开口方向,对称轴,顶点坐标,函数的增减性及最小值.
解答:解:∵y=x2-3x-4=(x-
)2-
,a=1>0,
∴抛物线的图象开口向上,对称轴是x=
,顶点坐标是(
,-
),
在对称轴的左侧,y随x的增大而减小,
当x=
时,函数y有最小值,是-
.
| 3 |
| 2 |
| 25 |
| 4 |
∴抛物线的图象开口向上,对称轴是x=
| 3 |
| 2 |
| 3 |
| 2 |
| 25 |
| 4 |
在对称轴的左侧,y随x的增大而减小,
当x=
| 3 |
| 2 |
| 25 |
| 4 |
点评:本题考查了二次函数的性质,将二次函数解析式的一般式转化为顶点式是解题的关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
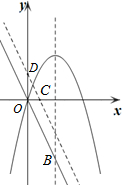 如图,一次函数y=-2x的图象与二次函数y=-x2+3x图象的对称轴交于点B.
如图,一次函数y=-2x的图象与二次函数y=-x2+3x图象的对称轴交于点B. 如图,将直线y=-2x沿y轴向上平移,分别交x轴、y轴于C、D两点.若点P是二次函数y=-x2+3x图象在y轴右侧部分上的一个动点,且以CD为直角边的△PCD与△OCD相似,则点P的坐标为
如图,将直线y=-2x沿y轴向上平移,分别交x轴、y轴于C、D两点.若点P是二次函数y=-x2+3x图象在y轴右侧部分上的一个动点,且以CD为直角边的△PCD与△OCD相似,则点P的坐标为