题目内容
如图，AB是⊙O的直径，弦CD交AB于点E，∠BAC=
∠BOD，若tan∠BOD=
，则tan∠BAC=（ ）
A．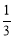
B． C．
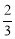D．
B．
【解析】
试题分析：：由于∠BAC=
∠BOD，则弧BC=弧BD，根据垂径定理的推论得到OB⊥CD，CE=DE，在Rt△ODE中，tan∠BOD=
，设DE=4x，则OE=3x，勾股定理得OD=5x，所以AE=8x，在Rt△ACE中，根据正切的定义求解．
试题解析：∵∠BAC=∠BOD，
∴
∴OB⊥CD，CE=DE，
在Rt△ODE中，tan∠BOD=，
设DE=4x，则OE=3x，
∴OD=
=5x，
∴AE=AO+OE=5x+3x=8x，CE=4x，
在Rt△ACE中，tan∠CAE=
，
∴tan∠BAC=
．
故选B．
考点：1.圆周角定理；2.垂径定理；3解直角三角形．
练习册系列答案
手拉手全优练考卷系列答案
相关题目
（
，
）满足
，则点
所在象限是（ ）
+4x+3只有一个交点，则a的值为 ．
（b，c是常数，且c<0）与x轴分别交于点A，B（点A位于点B的左侧），与y轴的负半轴交于点C，点A的坐标为（－1，0）．
． （2）
的最大值为