��Ŀ����
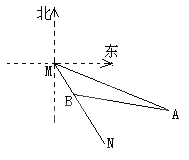
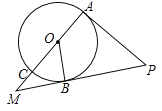
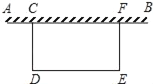
����Ŀ����ͼ��ijУ�㳡��һ��25�׳��ľ�Χ�����ִ������ø�Χ����һ���֣���ȫ����Ϊһ�ߣ�Χ��һ��100ƽ���ij����β�ƺ����ͼCDEF��CD��CF����֪����Χ���ļ۸���ÿ��1.75Ԫ������Χ���ļ۸���4.5Ԫ����CF��x�ף��ƻ�����ΪyԪ��
��1����y��x�ĺ�����ϵʽ����ָ��x��ȡֵ��Χ��
��2�����ƻ�����Ϊ150Ԫ���ܷ���ɸò�ƺΧ����������������ɣ���������þ�Χ�������ף���������ɣ���˵�����ɣ�
���𰸡���1��y��6.25x+![]() ��0��x��25������2��Ӧ���þ�Χ��12�ף�
��0��x��25������2��Ӧ���þ�Χ��12�ף�
��������
��1�������þ�Χ��CF�ij���Ϊx�ף���ô��Χ�����У�![]() ��2+x���ף������¾�Χ���ļ۸���֪�������y��x�ĺ�����ϵʽ��
��2+x���ף������¾�Χ���ļ۸���֪�������y��x�ĺ�����ϵʽ��
��2��y=150���루1���ĺ���ʽ�����x��
�⣺��1��y��1.75x+4.5��![]() ��2+x����
��2+x����
��1.75x+![]() +4.5x��
+4.5x��
��6.25x+![]() ��0��x��25����
��0��x��25����
��2����y��150ʱ��6.25x+![]() ��150
��150
�����ã�x2��24x+144��0
��ã�x1��x2��12
�����飬x��12��ԭ���̵Ľ⣬�ҷ������⣮
��Ӧ���þ�Χ��12�ף�

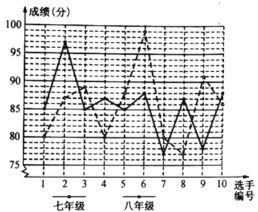
����Ŀ���ڳ��������������ļ�ֵ�ۡ��ݽ������У�ijУ���ݳ����ɼ����ߡ����꼶�ֱ�ѡ��10��ͬѧ�μӾ���������Щͬѧ�ľ����ɼ������������������Ƴ���������ɼ�ͳ�Ʊ���ѡ�ֳɼ�����ͳ��ͼ��
���꼶 | ���꼶 | |
ƽ���� | 85.7 | _______ |
���� | _______ | _______ |
���� | 37.4 | 27.8 |
��������ͼ���ṩ����Ϣ������������⣺
��1�����������ı�����д������
��2������ƽ�����뷽�����Ϊ�ĸ��꼶������ɼ����ã�
��3��������ÿ���꼶�ľ���ѡ���зֱ�ѡ��2���μӾ���������Ϊ�ĸ��꼶��ʵ����ǿһЩ����˵�����ɣ�