题目内容
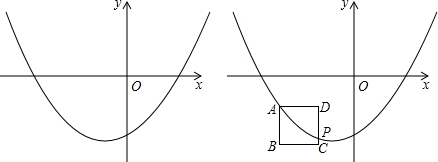
14.已知点A在二次函数y=$\frac{1}{2}$x2-bx-$\frac{3}{2}$(b为常数,b<0)的图象上,A点的横坐标为m,边长为1的正方形ABCD中,AB⊥x轴,点C在点A的右下方.(1)若A点坐标为(-2,-$\frac{1}{2}$),求二次函数图象的解析式;
(2)若反比例函数y=$\frac{k}{x}$(k>0,x>0)的图象与(1)中的抛物线在第一象限内交点的横坐标为x0,且满足$\frac{3}{2}$<x0<2,试确定整数k的值.
(3)若二次函数图象与CD边相交于点P(不与D点重合),求b-m的范围.
分析 (1)将A点坐代入解析式直接求出;
(2)利用反比例函数与二次函数在$\frac{3}{2}$<x<2这个范围内的增减性,得到x分别取两个端点值时的函数值的大小关系,从而得到关于k的不等式组,解得k的取值范围,取出范围内的整数解即可.
(3)用m表示出C、P、D三点的纵坐标,根据P点要处在C、D之间可列出两个不等式,化简整理即可.
解答 解:(1)将(-2,-$\frac{1}{2}$)代入二次函数解析式解得:b=-$\frac{1}{2}$,
二次函数的解析式为:y=$\frac{1}{2}$x2+$\frac{1}{2}$x-$\frac{3}{2}$;
(2)当$\frac{3}{2}$<x<2,
对于y=$\frac{1}{2}$x2+$\frac{1}{2}$x-$\frac{3}{2}$,y随着x的增大而增大,
对于y=$\frac{k}{x}$(k>0,x>0),y随着x的增大而减小.
所以当x=$\frac{3}{2}$时,由反比例函数图象在二次函数图象上方,
即:$\frac{2k}{3}>\frac{1}{2}×(\frac{3}{2})^{2}+\frac{1}{2}×\frac{3}{2}-\frac{3}{2}$,解得:$k>\frac{9}{16}$;
当x=2时,由二次函数图象在反比例函数图象上方,
即:$\frac{k}{2}<\frac{1}{2}×{2}^{2}+\frac{1}{2}×2-\frac{3}{2}$,解得:k<3,
∴$\frac{9}{16}<k<3$,
∵k是整数,
∴k=1,2;
(3)∵A点的横坐标为m,正方形ABCD边长为1,
∴A(m,$\frac{1}{2}{m}^{2}-bm-\frac{3}{2}$),
B(m,$\frac{1}{2}{m}^{2}-bm-\frac{5}{2}$),
C(m+1,$\frac{1}{2}{m}^{2}-bm-\frac{5}{2}$),
D(m+1,$\frac{1}{2}{m}^{2}-bm-\frac{3}{2}$),
P(m+1,$\frac{1}{2}{(m+1)}^{2}-b(m+1)-\frac{3}{2}$),
∵$\frac{1}{2}{m}^{2}-bm-\frac{5}{2}$≤$\frac{1}{2}{(m+1)}^{2}-b(m+1)-\frac{3}{2}$,
解得:b-m≤$\frac{3}{2}$,
∵$\frac{1}{2}{(m+1)}^{2}-b(m+1)-\frac{3}{2}$<$\frac{1}{2}{m}^{2}-bm-\frac{3}{2}$,
解得:b-m>$\frac{1}{2}$,
综上所述,$\frac{1}{2}$<b-m≤$\frac{3}{2}$.
点评 本题考查了待定系数法求二次函数解析式、二次函数和反比例函数在特定范围内的增减性、不等式与不等式组等重要知识点,有一点综合性,难度不大,但解法巧妙.第(2)问的关键是利用函数增减性列出不等式组,第(3)问的关键是利D、P、C三点的位置关系列出不等式组.

 步步高达标卷系列答案
步步高达标卷系列答案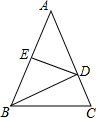 如图,在等腰△ABC中,DE是AB的垂直平分线.
如图,在等腰△ABC中,DE是AB的垂直平分线.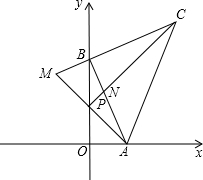 如图,在平面直角坐标系中,已知两点A(m,0),B(0,n)(n>m>0),点C在第一象限,AB⊥BC,BC=BA,点P在线段OB上,OP=OA,AP的延长线与CB的延长线交于点M,AB与CP交于点N.
如图,在平面直角坐标系中,已知两点A(m,0),B(0,n)(n>m>0),点C在第一象限,AB⊥BC,BC=BA,点P在线段OB上,OP=OA,AP的延长线与CB的延长线交于点M,AB与CP交于点N.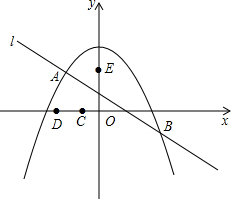 如图,以y轴为对称轴的抛物线y=ax2+k(a≠0)和直线l交于A(-2,3),B(4,-3)两点.
如图,以y轴为对称轴的抛物线y=ax2+k(a≠0)和直线l交于A(-2,3),B(4,-3)两点. 如图,将△ABC绕点B逆时针旋转90°后得到△A′BC′,则点A的对应点A′的坐标为(2,-3).
如图,将△ABC绕点B逆时针旋转90°后得到△A′BC′,则点A的对应点A′的坐标为(2,-3). 如图,AB为⊙O的直径,CD⊥AB于E,CO⊥AB于F,求证:AD=CD.
如图,AB为⊙O的直径,CD⊥AB于E,CO⊥AB于F,求证:AD=CD.