题目内容
如图，DE∥BC分别交AB、AC于D、E，（1）写出图中的相似三角形；
（2）求证：
| AD |
| AB |
| DO |
| CO |
分析：（1）由平行线可以判定△ADE∽△ABC，△DOE∽COB；
（2）利用（1）中的相似三角形性质：对应边的比值相等，即可证明
=
．
（2）利用（1）中的相似三角形性质：对应边的比值相等，即可证明
| AD |
| AB |
| DO |
| CO |
解答：（1）解：∵DE∥BC，
∴△ADE∽△ABC，△DOE∽COB；
（2）证明：∵△ADE∽△ABC，
∴
=
，
∵△DOE∽COB，
∴
=
，
∴
=
．
∴△ADE∽△ABC，△DOE∽COB；
（2）证明：∵△ADE∽△ABC，
∴
| AD |
| AB |
| DE |
| CB |
∵△DOE∽COB，
∴
| DE |
| CB |
| DO |
| CO |
∴
| AD |
| AB |
| DO |
| CO |
点评：本题考查了相似三角形的判定和性质，对于三角形相似的方法有事可单独使用，有时需要综合运用，无论是单独使用还是综合运用，都要具备应有的条件方可．
练习册系列答案
相关题目
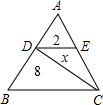如图，DE∥BC，△ADE、△DBC的面积值分别为2、8，求△DEC的面积值．
如图，DE∥BC分别交AB、AC于D、E，
．