Question

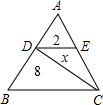如图，DE∥BC，△ADE、△DBC的面积值分别为2、8，求△DEC的面积值．

Answer 1

分析：先根据DE∥BC判断出△ADE∽△ABC，设相似比为n，△ADE的高为h，DE=y，则△ABC的高是nh，BC=ny，再根据S_△ADE=2，S_△BCD=8求出n的值，进而可得出△DCE的面积．

解答：解：∵DE∥BC，
∴△ADE∽△ABC，
设△ADE与△ABC的相似比为

1

n

，△ADE的高为h，DE=y，则△ABC的高是nh，BC=ny，
∵S_△ADE=2，S_△BCD=8，即

1

2

DE•h=

1

2

y•h=2①，

1

2

BC•（nh-h）=

1

2

ny•（nh-h）=8②，

①

②

得，

1

n(n-1)

=

1

4

，即n（n-1）=4，解得，n=

1+ 17

2

或n=

1- 17

2

（舍去），
∴

DE

BC

=n，
∵△ADE∽△ABC，
∴

S△ADE

S△ABC

=

2

8+x+2

=（

DE

BC

）²=（

2

1+ 17

）²，解得x=

17

-1，即S_△CDE=

17

-1．

点评：本题考查的是相似三角形的判定与性质，解答此题时要先设出相似三角形的相似比，再根据相似三角形面积的比等于相似比进行解答．