题目内容
【题目】如图,等腰三角形△ABC中,∠BAC=120°,AB=3.
(1)求BC的长.
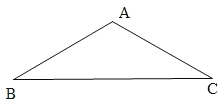
(2)如图,点D在CA的延长线上,DE⊥AB于E,DF⊥BC于F,连EF.求EF的最小值.
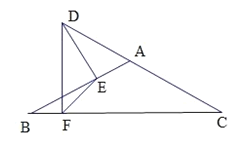
【答案】(1)BC=![]() ;(2)EF的最小值为
;(2)EF的最小值为![]()
【解析】
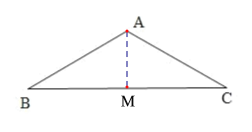
(1)过点A作AM⊥BC于点M,根据等腰三角形的性质得∠B=30°,BM=CM,由直角三角形的性质得BM=![]() ,进而即可求解;
,进而即可求解;
(2)连接BD,取BD的中点O,连接OE,OF,易得B,D,E,F四点共圆,从而得OEF是等边三角形,进而得EF=![]() BD,由BD⊥CD时, BD的值最小,进而即可求解.
BD,由BD⊥CD时, BD的值最小,进而即可求解.
(1)过点A作AM⊥BC于点M,
∵等腰三角形△ABC中,∠BAC=120°,AB=3,
∴∠B=(180°-120°)÷2=30°,BM=CM,
∴BM=3÷2×![]() =
=![]() ,
,
∴BC=2 BM=2×![]() =3
=3![]() ;
;
(2)连接BD,取BD的中点O,连接OE,OF,
∵DE⊥AB于E,DF⊥BC于F,
∴在RtBDF与RtBDE中,OB=OD=OE=OF=![]() BD,
BD,
∴B,D,E,F四点共圆,
∴∠EOF=2∠EBF=2×30°=60°,
∴OEF是等边三角形,
∴EF=OF=![]() BD,
BD,
∵∠C=∠EBF =30°,
∴当BD⊥CD时,BD=![]() BC=
BC=![]() ,此时,BD的值最小,
,此时,BD的值最小,
∴EF的最小值=![]() BD =
BD =![]() ×
×![]() =
=![]() .
.

练习册系列答案
相关题目
【题目】已知二次函数![]() 的
的![]() 与
与![]() 的部分对应值如下表:
的部分对应值如下表:
| -1 | 0 | 1 | 3 |
| -3 | 1 | 3 | 1 |
下列结论:①抛物线的开口向下;②其图象的对称轴为![]() ;③当
;③当![]() 时,函数值
时,函数值![]() 随
随![]() 的增大而增大;④方程
的增大而增大;④方程![]() 有一个根大于4.其中正确的结论有( )
有一个根大于4.其中正确的结论有( )
A.1个 B.2个 C.3个 D.4个