题目内容
【题目】如图,已知![]() ,
,![]() ,连接
,连接![]() ,过
,过![]() 点作
点作![]() 的垂线段
的垂线段![]() ,使
,使![]() ,连接
,连接![]() .
.
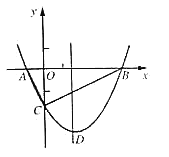
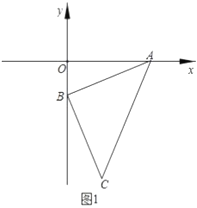
(1)如图1,求![]() 点坐标;
点坐标;
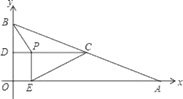
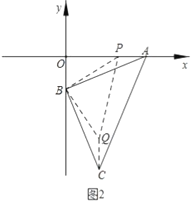
(2)如图2,若![]() 点从
点从![]() 点出发沿
点出发沿![]() 轴向左平移,连接
轴向左平移,连接![]() ,作等腰直角
,作等腰直角![]() ,连接
,连接![]() ,当点
,当点![]() 在线段
在线段![]() 上,求证:
上,求证:![]() ;
;
(3)在(2)的条件下若![]() 、
、![]() 、
、![]() 三点共线,求此时
三点共线,求此时![]() 的度数及
的度数及![]() 点坐标.
点坐标.
【答案】(1)![]() 点坐标为
点坐标为![]() ;(2)证明见解析;(3)∠APB=135°,
;(2)证明见解析;(3)∠APB=135°,![]() 点坐标为
点坐标为![]() .
.
【解析】
(1)作CH⊥y轴于H,证明△ABO≌△BCH,根据全等三角形的性质得到BH=OA=3,CH=OB=1,求出OH,得到C点坐标;
(2)证明△PBA≌△QBC,根据全等三角形的性质得到PA=CQ;
(3)根据C、P,Q三点共线,得到∠BQC=135![]() ,根据全等三角形的性质得到∠BPA=∠BQC=135
,根据全等三角形的性质得到∠BPA=∠BQC=135![]() ,根据等腰三角形的性质求出OP,得到P点坐标.
,根据等腰三角形的性质求出OP,得到P点坐标.
(1)作![]() 轴于
轴于![]() ,
,

则![]() ,
,
∵![]() ,
,
∴![]() ,
,
∴![]() ,
,
在![]() 和
和![]() 中,
中,
 ,
,
∴![]() ,
,
∴![]() ,
,![]() ,
,
∴![]() ,
,
∴![]() 点坐标为
点坐标为![]() ;
;
(2)∵![]() ,
,
∴![]() ,即
,即![]() ,
,
在![]() 和
和![]() 中,
中,
 ,
,
∴![]() ,
,
∴![]() ;
;
(3)∵![]() 是等腰直角三角形,∴
是等腰直角三角形,∴![]() ,
,
当![]() 、
、![]() 、
、![]() 三点共线时,
三点共线时,![]() ,
,
由(2)可知,![]() ,
,
∴![]() ,
,
∴![]() ,
,
∴![]() ,
,
∴![]() 点坐标为
点坐标为![]() .
.
故∠APB=135![]() ,
,![]() 点坐标为
点坐标为![]() .
.

练习册系列答案
 教材全解字词句篇系列答案
教材全解字词句篇系列答案
相关题目
【题目】下列图形都是由同样大小的菱形按照一定规律组成的,请根据排列规律完成下列问题:
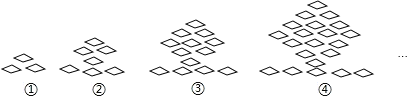
(1)填写下表:
图形序号 | 菱形个数 |
| 3 |
| 7 |
| ______ |
| ______ |
|
|
(2)根据表中规律猜想,图n中菱形的个数![]() 用含n的式子表示,不用说理
用含n的式子表示,不用说理![]() ;
;
(3)是否存在一个图形恰好由91个菱形组成?若存在,求出图形的序号;若不存在,说明理由.