题目内容
5.庄子说:“一尺之椎,日取其半,万世不竭”.这句话(文字语言)表达了古人将事物无限分割的思想,用图形语言表示为图1,按此图分割的方法,可得到一个等式(符号语言):1=$\frac{1}{2}$+$\frac{1}{2^2}$+$\frac{1}{2^3}$+…+$\frac{1}{2^n}$+….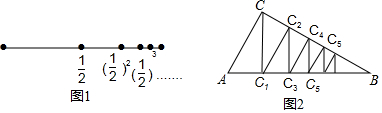
图2也是一种无限分割:在△ABC中,∠C=90°,∠B=30°,过点C作CC1⊥AB于点C1,再过点C1作C1C2⊥BC于点C2,又过点C2作C2C3⊥AB于点C3,如此无限继续下去,则可将利△ABC分割成△ACC1、△CC1C2、△C1C2C3、△C2C3C4、…、△Cn-2Cn-1Cn、….假设AC=2,这些三角形的面积和可以得到一个等式是2$\sqrt{3}$=$\frac{\sqrt{3}}{2}$$[1+\frac{3}{4}+(\frac{3}{4})^{2}+(\frac{3}{4})^{3}+…+(\frac{3}{4})^{n-1}+(\frac{3}{4})^{n}+…]$.
分析 先根据AC=2,∠B=30°,CC1⊥AB,求得S△ACC1=$\frac{\sqrt{3}}{2}$;进而得到${S}_{△C{C}_{1}{C}_{2}}$=$\frac{\sqrt{3}}{2}$×$\frac{3}{4}$,${S}_{△{C}_{1}{C}_{2}{C}_{3}}$=$\frac{\sqrt{3}}{2}$×($\frac{3}{4}$)2,${S}_{△{C}_{2}{C}_{3}{C}_{4}}$=$\frac{\sqrt{3}}{2}$×($\frac{3}{4}$)3,根据规律可知${S}_{△{C}_{n-2}{C}_{n-1}{C}_{n}}$=$\frac{\sqrt{3}}{2}$×($\frac{3}{4}$)n-1,再根据S△ABC=$\frac{1}{2}$AC×BC=$\frac{1}{2}$×2×2$\sqrt{3}$=2$\sqrt{3}$,即可得到等式.
解答 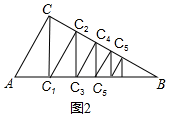 解:如图2,∵AC=2,∠B=30°,CC1⊥AB,
解:如图2,∵AC=2,∠B=30°,CC1⊥AB,
∴Rt△ACC1中,∠ACC1=30°,且BC=2$\sqrt{3}$,
∴AC1=$\frac{1}{2}$AC=1,CC1=$\sqrt{3}$AC1=$\sqrt{3}$,
∴S△ACC1=$\frac{1}{2}$•AC1•CC1=$\frac{1}{2}$×1×$\sqrt{3}$=$\frac{\sqrt{3}}{2}$;
∵C1C2⊥BC,
∴∠CC1C2=∠ACC1=30°,
∴CC2=$\frac{1}{2}$CC1=$\frac{\sqrt{3}}{2}$,C1C2=$\sqrt{3}$CC2=$\frac{3}{2}$,
∴${S}_{△C{C}_{1}{C}_{2}}$=$\frac{1}{2}$•CC2•C1C2=$\frac{1}{2}$×$\frac{\sqrt{3}}{2}$×$\frac{3}{2}$=$\frac{\sqrt{3}}{2}$×$\frac{3}{4}$,
同理可得,
${S}_{△{C}_{1}{C}_{2}{C}_{3}}$=$\frac{\sqrt{3}}{2}$×($\frac{3}{4}$)2,
${S}_{△{C}_{2}{C}_{3}{C}_{4}}$=$\frac{\sqrt{3}}{2}$×($\frac{3}{4}$)3,
…
∴${S}_{△{C}_{n-2}{C}_{n-1}{C}_{n}}$=$\frac{\sqrt{3}}{2}$×($\frac{3}{4}$)n-1,
又∵S△ABC=$\frac{1}{2}$AC×BC=$\frac{1}{2}$×2×2$\sqrt{3}$=2$\sqrt{3}$,
∴2$\sqrt{3}$=$\frac{\sqrt{3}}{2}$+$\frac{\sqrt{3}}{2}$×$\frac{3}{4}$+$\frac{\sqrt{3}}{2}$×($\frac{3}{4}$)2+$\frac{\sqrt{3}}{2}$×($\frac{3}{4}$)3+…+$\frac{\sqrt{3}}{2}$×($\frac{3}{4}$)n-1+…
∴2$\sqrt{3}$=$\frac{\sqrt{3}}{2}$$[1+\frac{3}{4}+(\frac{3}{4})^{2}+(\frac{3}{4})^{3}+…+(\frac{3}{4})^{n-1}+(\frac{3}{4})^{n}+…]$.
故答案为:2$\sqrt{3}$=$\frac{\sqrt{3}}{2}$$[1+\frac{3}{4}+(\frac{3}{4})^{2}+(\frac{3}{4})^{3}+…+(\frac{3}{4})^{n-1}+(\frac{3}{4})^{n}+…]$.
点评 本题主要考查了图形的变化类问题,解决问题的关键是找出图形哪些部分发生了变化,是按照什么规律变化的,通过分析找到各部分的变化规律后直接利用规律求解.探寻规律要认真观察、仔细思考,善用联想来解决这类问题.

| A. |  | B. |  | C. |  | D. |  |
| A. | 30=-3 | B. | a+2a=2a2 | C. | (ab2)3=a3b6 | D. | a6÷a2=a3 |
| A. | a≥-2 | B. | a≤2 | C. | a≥2 | D. | a≤-2 |
 如图,在四边形ABCD中,AD∥BC,∠B=90°,AD=8cm,BC=10cm,AB=6cm,点Q从点A出发以1cm/s的速度向点D运动,点P从点B出发以2cm/s的速度向点C运动,P、Q两点同时出发,当点P到达点C时,两点同时停止运动.若设运动时间为t(s)
如图,在四边形ABCD中,AD∥BC,∠B=90°,AD=8cm,BC=10cm,AB=6cm,点Q从点A出发以1cm/s的速度向点D运动,点P从点B出发以2cm/s的速度向点C运动,P、Q两点同时出发,当点P到达点C时,两点同时停止运动.若设运动时间为t(s)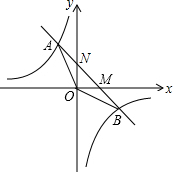 如图,已知一次函数y=kx+b的图象与反比例函数y=-$\frac{8}{x}$的图象交于A,B两点,且点A的横坐标和点B的纵坐标都是-2,求:
如图,已知一次函数y=kx+b的图象与反比例函数y=-$\frac{8}{x}$的图象交于A,B两点,且点A的横坐标和点B的纵坐标都是-2,求: