题目内容
17.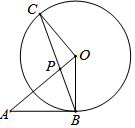 如图,AB与⊙O相切于点B,BC为⊙O的弦,OC⊥OA,OA与BC相交于点P.
如图,AB与⊙O相切于点B,BC为⊙O的弦,OC⊥OA,OA与BC相交于点P.(1)求证:AP=AB;
(2)若OB=4,AB=3,求线段BP的长.
分析 (1)欲证明AP=AB,只要证明∠APB=∠ABP即可;
(2)作OH⊥BC于H.在Rt△POC中,求出OP、PC、OH、CH即可解决问题.
解答 (1)证明:∵OC=OB,
∴∠OCB=∠OBC,
∵AB是⊙O的切线,
∴OB⊥AB,
∴∠OBA=90°,
∴∠ABP+∠OBC=90°,
∵OC⊥AO,
∴∠AOC=90°,
∴∠OCB+∠CPO=90°,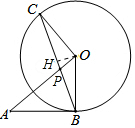
∵∠APB=∠CPO,
∴∠APB=∠ABP,
∴AP=AB.
(2)解:作OH⊥BC于H.
在Rt△OAB中,∵OB=4,AB=3,
∴OA=$\sqrt{{3}^{2}+{4}^{2}}$=5,
∵AP=AB=3,
∴PO=2.
在Rt△POC中,PC=$\sqrt{O{C}^{2}+O{P}^{2}}$=2$\sqrt{5}$,
∵$\frac{1}{2}$•PC•OH=$\frac{1}{2}$•OC•OP,
∴OH=$\frac{OC•OP}{PC}$=$\frac{4\sqrt{5}}{5}$,
∴CH=$\sqrt{O{C}^{2}-O{H}^{2}}$=$\frac{8\sqrt{5}}{5}$,
∵OH⊥BC,
∴CH=BH,
∴BC=2CH=$\frac{16\sqrt{5}}{5}$,
∴PB=BC-PC=$\frac{16\sqrt{5}}{5}$-2$\sqrt{5}$=$\frac{6\sqrt{5}}{5}$.
点评 本题考查切线的性质、解直角三角形、勾股定理、等腰三角形的判定和性质、垂径定理等知识,解题的关键是学会添加常用辅助线,构造直角三角形解决问题,属于中考常考题型.

练习册系列答案
 金牌教辅培优优选卷期末冲刺100分系列答案
金牌教辅培优优选卷期末冲刺100分系列答案
相关题目
3.在一个不透明的盒子里装着除颜色外完全相同的黑、白两种颜色的小球共40个,程程做摸球实验,她将盒子里面的小球搅匀后从中随机摸出一个小球,记下颜色后放回,不断重复上述过程,多次实验后,得到表中的数据,则盒子里的白球最可能有( )
| 摸球的次数n | 100 | 200 | 300 | 500 | 800 | 1000 | 3000 |
| 摸到白球的次数m | 62 | 122 | 179 | 302 | 481 | 599 | 1810 |
| A. | 30个 | B. | 28个 | C. | 24个 | D. | 16个 |
10.能用平方差公式计算的是( )
| A. | (-x+2y)(x-2y) | B. | (2x-y)(2y+x) | C. | (m-n)(n-m) | D. | 99×101 |
 在“三角尺拼角”实验中,小明同学把一副三角尺按如图所示的方式放置,则∠1=120°.
在“三角尺拼角”实验中,小明同学把一副三角尺按如图所示的方式放置,则∠1=120°.
 如图,正方形ABCD的边长为3,点E在边AB上,且BE=1,若点P在对角线BD上移动,则PA+PE的最小值是$\sqrt{10}$.
如图,正方形ABCD的边长为3,点E在边AB上,且BE=1,若点P在对角线BD上移动,则PA+PE的最小值是$\sqrt{10}$.