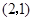题目内容
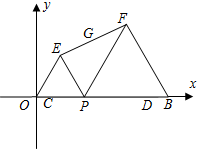 如图,C、D、B的坐标分别为(1,0)(9,0)(10,0),点P(t,0)是CD上一个动点,在x轴上方作等边△OPE和△BPF,连EF,G为EF的中点.
如图,C、D、B的坐标分别为(1,0)(9,0)(10,0),点P(t,0)是CD上一个动点,在x轴上方作等边△OPE和△BPF,连EF,G为EF的中点.
(1)当t=______时,EF∥OB;
(2)双曲线y= 过点G,当PG=
过点G,当PG=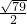 时,则k=______.
时,则k=______.
解:(1)作EM⊥OB于M点,FN⊥OB于N点,如图,
∵△OPE和△BPF都是等边三角形,
∴EM= OP,FN=
OP,FN= PB,
PB,
当EM=FN时,EF∥OB,
∵P(t,0),B(10,0),
∴PC=t,PB=10-t
∴ t=
t= (10-t),
(10-t),
∴t=5;
(2)作GH⊥OB于H点,如图,
∵G为EF的中点,
∴GH为梯形EMNF的中位线,
∴GH= (EM+FN)=
(EM+FN)= [
[ t+
t+ (10-t)]=
(10-t)]= ,HM=
,HM= MN=
MN= (ON-OM)=
(ON-OM)= [t+
[t+ (10-t)-
(10-t)- t]=
t]= ,
,
∴PH= -
- t或
t或 t-
t- ,
,
在Rt△PGH中,PG2=GH2+PH2,
∴( )2+(
)2+(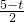 )2=(
)2=(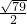 )2,
)2,
∴t1=3,t2=7,
当t=3时,OH= +
+ t=4,
t=4,
∴G点坐标为(4, ),
),
把G(4, )代入y=
)代入y= 得k=4×
得k=4× =10
=10 ;
;
当t=7时,OH= +
+ =6,
=6,
∴G点坐标为(6, ),
),
把G(6, )代入y=
)代入y= 得k=6×
得k=6× =15
=15 ;
;
∴k的值为10 或15
或15 .
.
故答案为5;10 或15
或15 .
.
分析:(1)作EM⊥OB于M点,FN⊥OB于N点,根据等边三角形的性质得EM= OP,FN=
OP,FN= PB,所以EM=FN时,EF∥OB,则
PB,所以EM=FN时,EF∥OB,则 t=
t= (10-t),然后即方程即可得到t的值;
(10-t),然后即方程即可得到t的值;
(2)作GH⊥OB于H点,则GH为梯形EMNF的中位线,根据梯形中位线的性质得GH= (EM+FN)=
(EM+FN)= ,HM=
,HM= MN=
MN= (ON-OM)=
(ON-OM)= ,得到PH=
,得到PH= -
- t或
t或 t-
t- ,
,
再利用勾股定理得PG2=GH2+PH2,即( )2+(
)2+(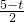 )2=(
)2=(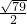 )2,解得t1=3,t2=7,然后分别确定G点坐标,再代入反比例函数解析式可得到k的值.,
)2,解得t1=3,t2=7,然后分别确定G点坐标,再代入反比例函数解析式可得到k的值.,
点评:本题考查了反比例函数的综合题:反比例函数图象上点的坐标满足其函数解析式,运用待定系数法求函数的解析式;掌握等边三角形的性质、含30°的直角三角形三边的关系和勾股定理.
∵△OPE和△BPF都是等边三角形,

∴EM=
 OP,FN=
OP,FN= PB,
PB,当EM=FN时,EF∥OB,
∵P(t,0),B(10,0),
∴PC=t,PB=10-t
∴
 t=
t= (10-t),
(10-t),∴t=5;
(2)作GH⊥OB于H点,如图,
∵G为EF的中点,
∴GH为梯形EMNF的中位线,
∴GH=
 (EM+FN)=
(EM+FN)= [
[ t+
t+ (10-t)]=
(10-t)]= ,HM=
,HM= MN=
MN= (ON-OM)=
(ON-OM)= [t+
[t+ (10-t)-
(10-t)- t]=
t]= ,
,∴PH=
 -
- t或
t或 t-
t- ,
,在Rt△PGH中,PG2=GH2+PH2,
∴(
 )2+(
)2+(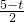 )2=(
)2=(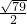 )2,
)2,∴t1=3,t2=7,
当t=3时,OH=
 +
+ t=4,
t=4,∴G点坐标为(4,
 ),
),把G(4,
 )代入y=
)代入y= 得k=4×
得k=4× =10
=10 ;
;当t=7时,OH=
 +
+ =6,
=6,∴G点坐标为(6,
 ),
),把G(6,
 )代入y=
)代入y= 得k=6×
得k=6× =15
=15 ;
;∴k的值为10
 或15
或15 .
.故答案为5;10
 或15
或15 .
.分析:(1)作EM⊥OB于M点,FN⊥OB于N点,根据等边三角形的性质得EM=
 OP,FN=
OP,FN= PB,所以EM=FN时,EF∥OB,则
PB,所以EM=FN时,EF∥OB,则 t=
t= (10-t),然后即方程即可得到t的值;
(10-t),然后即方程即可得到t的值;(2)作GH⊥OB于H点,则GH为梯形EMNF的中位线,根据梯形中位线的性质得GH=
 (EM+FN)=
(EM+FN)= ,HM=
,HM= MN=
MN= (ON-OM)=
(ON-OM)= ,得到PH=
,得到PH= -
- t或
t或 t-
t- ,
,再利用勾股定理得PG2=GH2+PH2,即(
 )2+(
)2+(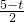 )2=(
)2=(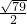 )2,解得t1=3,t2=7,然后分别确定G点坐标,再代入反比例函数解析式可得到k的值.,
)2,解得t1=3,t2=7,然后分别确定G点坐标,再代入反比例函数解析式可得到k的值.,点评:本题考查了反比例函数的综合题:反比例函数图象上点的坐标满足其函数解析式,运用待定系数法求函数的解析式;掌握等边三角形的性质、含30°的直角三角形三边的关系和勾股定理.

练习册系列答案
 新课标阶梯阅读训练系列答案
新课标阶梯阅读训练系列答案 口算心算速算应用题系列答案
口算心算速算应用题系列答案 同步拓展阅读系列答案
同步拓展阅读系列答案
相关题目
 (2013•南昌)一张坐凳的形状如图所示,以箭头所指的方向为主视方向,则它的左视图可以是( )
(2013•南昌)一张坐凳的形状如图所示,以箭头所指的方向为主视方向,则它的左视图可以是( )
 一种长方形餐桌的四周可坐6人用餐.现把n张这样的餐桌按如图方式拼接起来,问四周可坐多少人用餐?若用餐的人数有18人,则需要这样的餐桌多少张?
一种长方形餐桌的四周可坐6人用餐.现把n张这样的餐桌按如图方式拼接起来,问四周可坐多少人用餐?若用餐的人数有18人,则需要这样的餐桌多少张?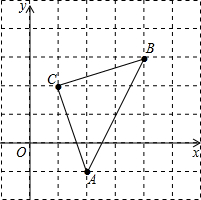 如图,直角坐标系中,△ABC的顶点都在网格点上,其中C点坐(1,2)
如图,直角坐标系中,△ABC的顶点都在网格点上,其中C点坐(1,2)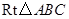 绕点
绕点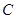 按顺时针方向旋转
按顺时针方向旋转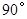 ,得到
,得到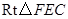 ,则点
,则点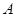 的对应点
的对应点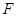 的坐 标是
的坐 标是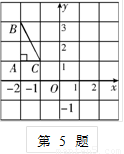
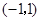 B.
B.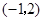 C.
C.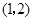 D.
D.