题目内容
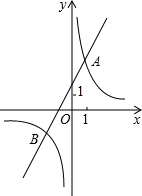
如图，点O是△ABC的内切圆的圆心，若∠BAC=80°，则∠BOC=（ ）
A．130° B．100° C．50° D．65°
A【考点】三角形的内切圆与内心．
【专题】压轴题．
【分析】由三角形内切定义可知：OB、OC是∠ABC、∠ACB的角平分线，利用三角形内角和定理和角平分线的性质可得∠OBC+∠OCB=
（∠ABC+∠ACB），把对应数值代入即可求得∠BOC的值．
【解答】解：∵OB、OC是∠ABC、∠ACB的角平分线，
∴∠OBC+∠OCB=（∠ABC+∠ACB）==50°，
∴∠BOC=180°﹣50°=130°．
故选A．
【点评】本题通过三角形内切圆，考查切线的性质．
练习册系列答案
相关题目
.
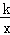的图象与一次函数y2=ax+b的图象交于点A（1，4）和点（m，﹣2），则满足y1＞y2的自变量x的取值范围是__________．