题目内容
9．估计2$\sqrt{3}$与$\sqrt{11}$的大小关系：2$\sqrt{3}$＞$\sqrt{11}$（填“＞”、“＜”或“=”）．分析 将两数分别平方，因为两数均大于0，所以平方大的数本身就大．
解答 解：${（2\sqrt{3}）}^{2}$=4×3=12，${（\sqrt{11}）}^{2}$=11，
∵2$\sqrt{3}$＞0，$\sqrt{11}$＞0，12＞11，
∴2$\sqrt{3}$＞$\sqrt{11}$．
故答案为：＞．
点评 本题考查的是实数比较大小，解题的关键是将两数平方后进行比较，由两数本身大于0，故平方大的数本身也大．
练习册系列答案
相关题目
19．下列叙述正确的是（ ）??
| A． | 任意两个等腰三角形相似 | |
| B． | 任意两个等腰直角三角形相似 | |
| C． | 两个全等三角形不相似 | |
| D． | 两个相似三角形的相似比不可能等于1 |
20．运用平方差公式计算，错误的是（ ）
| A． | （a+b）（a-b）=a2-b2 | B． | （x+1）（x-1）=x2-1 | C． | （-a+b）（-a-b）=a2-b2 | D． | （2x+1）（2x-1）=2x2-1 |
如图，AB、CD、EF是与路灯在同一直线上的三个等高的标杆，相邻的两个标杆之间的距离都是2m，已知AB、CD在路灯光下的影长分别为BM=1.6m，DN=0.6m．求标杆EF的影长．
1．下列四个数中，在-2到-1之间的数是（ ）
| A． | -1 | B． | $-\frac{1}{2}$ | C． | $-\frac{3}{2}$ | D． | 0 |
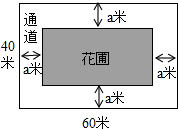如图，为美化校园环境，某校计划在一块长为60米，宽为40米的长方形空地上修建一个长方形花圃，并将花圃四周余下的空地修建成同样宽的通道，设通道宽为a米．