Question

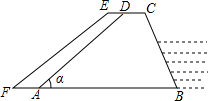如图，梯形ABCD是一个拦河坝的截面图，坝高为6米．背水坡AD的坡角α为45°，为了提高河坝的抗洪能力，防汛指挥部决定加固河坝，若坝顶CD加宽0.8米，新的背水坡EF的坡度为1：1.4．河坝总长度为500米．
（1）求完成该工程需要多少立方米方土？
（2）某工程队在加固600立方米土后，采用新的加固模式，这样每天加固方数是原来的2倍，结果只用11天完成了大坝加固的任务．请你求出该工程队原来每天加固多少立方米土？

Answer 1

分析：（1）过点D作DG⊥AB于G，过点E作EH⊥AB于H，由CD与AB平行，得到两垂线段相等，再由α为4°，求出AG=DG=EH，根据EF坡度求出FH的长，由FH+GH-AG求出FA的长，利用梯形面积公式求出梯形ADEF面积，即可确定出土方；
（2）设原来每天加固x米，根据题意列出关于x的分式方程，去分母转化为整式方程，求出整式方程的解得到x的值，经检验即可得到结果．

解答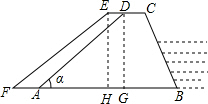：解：（1）过点D作DG⊥AB于G，过点E作EH⊥AB于H，
∵CD∥AB，
∴EH=DG=6米，
∵tan45°=

DG

AG

，
∴AG=6米，
∵

EH

FH

=

1

1.4

，
∴FH=8.4米，
∴FA=FH+GH-AG=8.4+0.8-6=3.2（米），
∴S_梯形ADEF=

1

2

（ED+FA）•EH=

1

2

×（0.8+3.2）×6=12，
∴V=12×500=6000（立方米）；     
              
（2）设原来每天加固x米，根据题意，
得：

600

x

+

6000-600

2x

=11，
去分母，得 1200+5400=22x，
解得：x=300，
检验：当x=300时，2x≠0（或分母不等于0），
∴x=300是原方程的解．                                   
答：该工程队原来每天加固300米．

点评：此题考查了解直角三角形-坡度坡角问题，以及分式方程的应用，弄清题意是解本题的关键．