题目内容
9.(1)解方程组$\left\{\begin{array}{l}{2m-n=6}\\{m+2n=-2}\end{array}\right.$(2)解不等式组$\left\{\begin{array}{l}{1+x>-2}\\{\frac{2x-1}{3}≤1}\end{array}\right.$,并把它的解集在数轴上表示出来.
分析 (1)加减消元法求解可得;
(2)分别求出每一个不等式的解集,根据口诀:同大取大、同小取小、大小小大中间找、大大小小无解了确定不等式组的解集.
解答 解:(1)$\left\{\begin{array}{l}{2m-n=6}&{①}\\{m+2n=-2}&{②}\end{array}\right.$,
①×2+②,得:5m=10,
解得:m=2,
将m=2代入②,得:2+2n=-2,
解得:n=-2,
∴方程组的解为$\left\{\begin{array}{l}{m=2}\\{n=-2}\end{array}\right.$;
(2)解不等式1+x>-2,得:x>-3,
解不等式$\frac{2x-1}{3}$≤1,得:x≤2,
则不等式组的解集为-3<x≤2,
将解集表示在数轴上如下:
点评 本题考查的是解二元一次方程组和解一元一次不等式组,正确求出每一个不等式解集是基础,熟知“同大取大;同小取小;大小小大中间找;大大小小找不到”的原则和加减消元法是解答此题的关键

练习册系列答案
相关题目
19.已知实数a,b,c满足a+b+c=0且a<b<c.则一次函数y=($\frac{c}{a}$+2)x+$\frac{b}{c}$的图象一定经过( )
| A. | 第一、三象限 | B. | 第二、四象限 | C. | 第一、三、四象限 | D. | 第一、二、三象限 |
17.下列问题,不适合用全面调查的是( )
| A. | 旅客上飞机前的安全检查 | B. | 学校招聘教师,对应聘人员的面试 | ||
| C. | 了解一批灯管的使用寿命 | D. | 了解全班学生的课外读书时间 |
19.已知m,n分别是一个三角形的底和该底上的高,且满足(m-n)2=5,(m+n)2=11,则此三角形的面积为( )
| A. | 24 | B. | 12 | C. | $\frac{3}{2}$ | D. | $\frac{3}{4}$ |
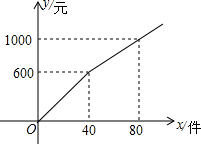 梅梅以每件6元的价格购进某商品若干件到市场去销售,销售金额y(元)与销售量x(件)的函数关系图象如图所示,则降价后每件商品的销售利润为( )
梅梅以每件6元的价格购进某商品若干件到市场去销售,销售金额y(元)与销售量x(件)的函数关系图象如图所示,则降价后每件商品的销售利润为( )



