题目内容
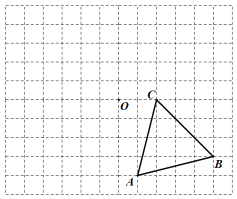
【题目】如图,在平面直角坐标系中,抛物线![]() 与x轴交于B(-3,0)、C(1,0)两点,与y轴交于点A(0,2),抛物线的顶点为D.连接AB,点E是第二象限内的抛物线上的一动点,过点E作EP⊥BC于点P,交线段AB于点F.
与x轴交于B(-3,0)、C(1,0)两点,与y轴交于点A(0,2),抛物线的顶点为D.连接AB,点E是第二象限内的抛物线上的一动点,过点E作EP⊥BC于点P,交线段AB于点F.
(1)求此抛物线的解析式;
(2)过点E作EG⊥AB于点G,Q为线段AC的中点,当△EGF周长最大时,在![]() 轴上找一点R,使得|RE-RQ|值最大,请求出R点的坐标及|RE-RQ|的最大值;
轴上找一点R,使得|RE-RQ|值最大,请求出R点的坐标及|RE-RQ|的最大值;

(3)在(2)的条件下,将△PED绕E点旋转得△ED′P′,当△AP′P是以AP为直角边的直角三角形时,求点P′的坐标.

【答案】(1)![]() ;(2)E(
;(2)E(![]() ,
, ![]() ),R(
),R(![]() ,0),最大值为
,0),最大值为![]() ;(3)P′(
;(3)P′(![]() ,
, ![]() )或(
)或(![]() ,
, ![]() )或(
)或(![]() ,
, ![]() ).
).
【解析】试题分析:(1)把A、B、C的坐标代入抛物线解析式,求出a、b、c的值即可得出解析式;
(2)先证△EFG∽△BAO,得![]() ,所以当EF最大时△EFG周长最大,求出AB的解析式,设出点E、F的坐标,表示出EF的长,求出EF最大时E点坐标,根据中点坐标求法求出点Q坐标,表示出EQ的解析式,当E、Q、R在同一直线上时|RE-RQ|最大,求出此时R点坐标和EQ的长即为答案;
,所以当EF最大时△EFG周长最大,求出AB的解析式,设出点E、F的坐标,表示出EF的长,求出EF最大时E点坐标,根据中点坐标求法求出点Q坐标,表示出EQ的解析式,当E、Q、R在同一直线上时|RE-RQ|最大,求出此时R点坐标和EQ的长即为答案;
(3)用待定系数法求出PA的解析式为y=![]() ,
,
①当∠P’PA=90°时,根据相互垂直的两条直线比例系数互为负倒数求出PP’的解析式为y=![]() ,设P’(x,
,设P’(x, ![]() ),由EP’=EP列方程求出x的值,即可得出点P’的坐标;
),由EP’=EP列方程求出x的值,即可得出点P’的坐标;
②当∠PAP’=90°时,同理求出AP’的解析式,利用前面的方法即可得出点P’的坐标.
试题解析:
解:(1)∵抛物线经过点A(0,2)、B(-3,0)、C(1,0),
∴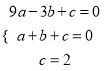 ,
,
解得: 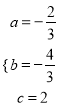 ,
,
∴抛物线的解析式为:y=![]() ;
;
(2)∵EG⊥AB,EP⊥OB,
∴∠EGF=∠FPB=90°,
∴∠E+∠EFG=90°,∠PBF+∠BFP=90°,
∵∠EFG=∠BFP,
∴∠E=∠PBF,
又∠EGF=∠AOB,
∴△EFG∽△BAO,
∴![]() ,
,
∵AB是定值,
∴当EF最大时△EFG周长最大,
设AB的解析式为y=kx+b,
则有![]() ,
,
解得 ,
,
∴AB的解析式为y=![]() x+2,
x+2,
设E(x, ![]() ),则F(x,
),则F(x, ![]() x+2).
x+2).
∴EF=(![]() )-(
)-(![]() x+2)=
x+2)= ![]() =
=![]() ,
,
当x=![]() 时EF有最大值,
时EF有最大值,
此时E(![]() ,
, ![]() ).
).
∵Q是AC中点,A(0,2),C(1,0),
∴Q(![]() ,1),
,1),
EQ的解析式为:y=![]() ,
,
当E、Q、R在同一直线上时|RE-RQ|最大,
令y=0,则![]() =0,
=0,
x=![]() ,
,
∴R(![]() ,0),
,0),
此时|RE-RQ|最大值=EQ=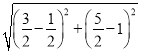 =
=![]() ;
;
(3)∵EP⊥x轴,E(![]() ,
, ![]() ),
),
∴P(![]() ,0),
,0),
∵A(0,2),
∴PA的解析式为y=![]() ,
,
①当∠P’PA=90°时,
设PP’的解析式为y=![]() ,
,
把P(![]() ,0)代入得b=
,0)代入得b=![]() ,
,
∴PP’的解析式为y=![]() ,
,
设P’(x, ![]() ),
),
∵EP’=EP,
∴![]() ,
,
解得:x1=![]() ,x2=
,x2=![]() (不符合题意,舍去),
(不符合题意,舍去),
![]() =
=![]() ,
,
∴P’( ![]() ,
, ![]() );
);
②当∠PAP’=90°时,
同理可得AP’的解析式为:y=![]() ,
,
设P’(x, ![]() ),
),
∵EP’=EP,
∴![]() ,
,
解得:x1=![]() ,x2=
,x2=![]() ,
,
当x=![]() 时,
时, ![]() =
=![]() ,
,
当x=![]() 时,
时, ![]() =
=![]() ,
,
∴P’( ![]() ,
, ![]() )或(
)或(![]() ,
, ![]() ).
).
综上P’ (![]() ,
, ![]() )或(
)或( ![]() ,
, ![]() )或(
)或(![]() ,
, ![]() ).
).

 名校课堂系列答案
名校课堂系列答案