题目内容
 如图,A、B是⊙O上的两点,AC是⊙O的切线,∠OBA=75°,⊙O的半径为1,则OC的长等于
如图,A、B是⊙O上的两点,AC是⊙O的切线,∠OBA=75°,⊙O的半径为1,则OC的长等于
- A.

- B.

- C.

- D.

C
分析:由OA=OB可以得到∠OBA的度数,然后求出∠AOC.设BC的长为x,再利用三角函数将AC的长用含x的代数式表示出来.在Rt△OAC中,运用勾股定理可将BC的长求出,进而可将OC的长求出.
解答:设BC的长为x,则OC的长为1+x,
∵OA=OB,∠OBA=75°,
∴∠AOC=180°-75°×2=30°.
∴AC=sin∠AOC×OC= (1+x).
(1+x).
在Rt△OAC中,OC2=OA2+AC2
即(1+x)2=12+(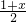 )2
)2
∴x=-1+ (舍负值).
(舍负值).
∴OC=OB+BC= .
.
故选C.
点评:本题考查了圆的切线性质,勾股定理及解直角三角形的知识,关键是利用勾股定理列出方程.
分析:由OA=OB可以得到∠OBA的度数,然后求出∠AOC.设BC的长为x,再利用三角函数将AC的长用含x的代数式表示出来.在Rt△OAC中,运用勾股定理可将BC的长求出,进而可将OC的长求出.
解答:设BC的长为x,则OC的长为1+x,
∵OA=OB,∠OBA=75°,
∴∠AOC=180°-75°×2=30°.
∴AC=sin∠AOC×OC=
 (1+x).
(1+x).在Rt△OAC中,OC2=OA2+AC2
即(1+x)2=12+(
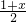 )2
)2∴x=-1+
 (舍负值).
(舍负值).∴OC=OB+BC=
 .
.故选C.
点评:本题考查了圆的切线性质,勾股定理及解直角三角形的知识,关键是利用勾股定理列出方程.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
 如图,A、D是⊙O上的两个点,BC是直径,若∠D=35°,则∠OAC等于( )
如图,A、D是⊙O上的两个点,BC是直径,若∠D=35°,则∠OAC等于( )| A、65° | B、35° | C、70° | D、55° |
 如图,A、B是⊙O上的两点,AC是⊙O的切线,∠OBA=75°,⊙O的半径为1,则OC的长等于( )
如图,A、B是⊙O上的两点,AC是⊙O的切线,∠OBA=75°,⊙O的半径为1,则OC的长等于( )A、
| ||||
B、
| ||||
C、
| ||||
D、
|
 20、已知:如图,E、F是AB上的两点,AE=BF,AC∥BD,∠C=∠D.求证:CF=DE.
20、已知:如图,E、F是AB上的两点,AE=BF,AC∥BD,∠C=∠D.求证:CF=DE. (2012•南京)如图,A、B是⊙O上的两个定点,P是⊙O上的动点(P不与A、B重合)、我们称∠APB是⊙O上关于点A、B的滑动角.
(2012•南京)如图,A、B是⊙O上的两个定点,P是⊙O上的动点(P不与A、B重合)、我们称∠APB是⊙O上关于点A、B的滑动角.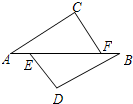 已知:如图,E、F是AB上的两点,AC=BD,AC∥BD,∠C=∠D;
已知:如图,E、F是AB上的两点,AC=BD,AC∥BD,∠C=∠D;