题目内容
阅读探索:“任意给定一个矩形A,是否存在另一个矩形B,它的周长和面积分别是已知矩形周长和面积的一半?”(完成下列空格)(1)当已知矩形A的边长分别为6和1时,小亮同学是这样研究的:
设所求矩形的两边分别是x和y,由题意得方程组:
|
∵△=49-48>0,∴x1=
∴满足要求的矩形B存在.
(2)如果已知矩形A的边长分别为2和1,请你仿照小亮的方法研究是否存在满足要求的矩形B.
(3)如果矩形A的边长为m和n,请你研究满足什么条件时,矩形B存在?
分析:(1)直接利用求根公式计算即可;
(2)参照(1)中的解法解题即可;
(3)解法同上,利用根的判别式列不等关系可求m,n满足的条件.
(2)参照(1)中的解法解题即可;
(3)解法同上,利用根的判别式列不等关系可求m,n满足的条件.
解答:解:(1)由上可知
(x-2)(2x-3)=0
∴x1=2,x2=
;
(2)设所求矩形的两边分别是x和y,由题意,得
消去y化简,得
2x2-3x+2=0
∵△=9-16<0
∴不存在矩形B;
(3)(m+n)2-8mn≥0.
设所求矩形的两边分别是x和y,由题意,得
消去y化简,得
2x2-(m+n)x+mn=0
△=(m+n)2-8mn≥0
即(m+n)2-8mn≥0时,满足要求的矩形B存在.
(x-2)(2x-3)=0
∴x1=2,x2=
| 3 |
| 2 |
(2)设所求矩形的两边分别是x和y,由题意,得
|
消去y化简,得
2x2-3x+2=0
∵△=9-16<0
∴不存在矩形B;
(3)(m+n)2-8mn≥0.
设所求矩形的两边分别是x和y,由题意,得
|
消去y化简,得
2x2-(m+n)x+mn=0
△=(m+n)2-8mn≥0
即(m+n)2-8mn≥0时,满足要求的矩形B存在.
点评:此类题目要读懂题意,准确的找到等量关系列方程组,要会灵活运用根的判别式在不解方程的情况下判断一元二次方程的解的情况.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 ,由题意得方程组:
,由题意得方程组: ,
, ,
,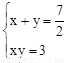 ,
,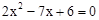 ,
,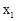 =
,
=
,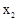 =
.
=
. ,由题意得方程组:
,由题意得方程组: ,
, ,
, ,
,