题目内容
2.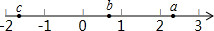 有理数a、b、c在数轴上的位置如图所示:
有理数a、b、c在数轴上的位置如图所示:(1)判断正负,用“>”或“<”填空:b-c>0;b-a<0;a+c>0.
(2)化简:|b-c|-|b-a|+|a+c|+|c|.
分析 (1)根据有理数的加减法,可得答案;根据绝对值的意义,可得答案;
(2)根据绝对值的性质,可化简去掉绝对值,根据合并同类项,可得答案.
解答 解:(1)用“>、=或<”填空:,
b-c>0; b-a<0; a+c>0.
故答案为:>,<,>;
(2)原式=(c-b)-(a-b)+(a+c)+(-c)
=b-c-a+b+a+c-c
=2b-c.
点评 本题考查了合并同类项,利用绝对值的性质化简绝对值,利用合并同类项得出答案.

练习册系列答案
 新课标阶梯阅读训练系列答案
新课标阶梯阅读训练系列答案 口算心算速算应用题系列答案
口算心算速算应用题系列答案
相关题目
10.二次根式$\sqrt{x-4}$有意义,则x的取值范围是( )
| A. | x≥4 | B. | x>4 | C. | x<4 | D. | x≤4 |
7. 在小孔成像问题中,根据如图所示,若O到AB的距离是18cm,O到CD的距离是6cm,则像CD的长是物AB长的( )
在小孔成像问题中,根据如图所示,若O到AB的距离是18cm,O到CD的距离是6cm,则像CD的长是物AB长的( )
 在小孔成像问题中,根据如图所示,若O到AB的距离是18cm,O到CD的距离是6cm,则像CD的长是物AB长的( )
在小孔成像问题中,根据如图所示,若O到AB的距离是18cm,O到CD的距离是6cm,则像CD的长是物AB长的( )| A. | 3倍 | B. | $\frac{1}{2}$ | ||
| C. | $\frac{1}{3}$ | D. | 不知AB的长度,无法判断 |
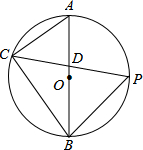 如图,AB是⊙O的直径,点P是$\widehat{AB}$的中点.
如图,AB是⊙O的直径,点P是$\widehat{AB}$的中点. 如图,要使过点A的射线AD∥BC,可以添加一个条件是∠DAB=∠B.
如图,要使过点A的射线AD∥BC,可以添加一个条件是∠DAB=∠B.