题目内容
7．
如图，△ABC是等边三角形，延长BA至点D，延长CB至点E，使得BE=AD，连结CD，AE．求证：AE=CD．
分析 只要证明△ABE≌△ACD，即可推出AE=CD．
解答 证明：∵△ABC是等边三角形，
∴AB=AC，∠CAB=∠ABC=60°，
∴∠DAC=∠ABE=120°，
在△ABE和△ACD中，
$\left\{\begin{array}{l}{AB=AC}\\{∠ABE=∠CAD}\\{BE=AD}\end{array}\right.$，
∴△ABE≌△ACD，
∴AE=CD．
点评 本题考查等边三角形的性质、全等三角形的判定和性质等知识，解题的关键是灵活运用所学知识，属于基础题，中考常考题型．
练习册系列答案
相关题目
17．计算（x+y）（y-x）=（ ）
| A． | x2-y2 | B． | x2+y2 | C． | y2-x2 | D． | （x-y）2 |
15．下列计算结果正确的是（ ）
| A． | 2+$\sqrt{5}$=2$\sqrt{5}$ | B． | $\sqrt{6}$÷$\sqrt{2}$=$\sqrt{3}$ | C． | （-2a2）3=-6a6 | D． | （x+1）2=x2+1 |
12．若分式$\frac{x+2}{x-2}$的值为0，则x的取值应满足是（ ）
| A． | x=-2 | B． | x≠-2 | C． | x=2 | D． | x≠2 |
19．下列分式的变形正确的是（ ）
| A． | $\frac{a}{a-1}-\frac{1}{a-1}=1$ | B． | $\frac{m}{{{m^2}+1}}=\frac{1}{m+1}$ | C． | $\frac{{{x^2}-1}}{x-1}=x-1$ | D． | $\frac{-a-1}{a+1}=-\frac{a-1}{a+1}$ |
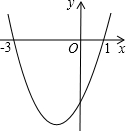如图，二次函数y=ax2+bx+c的图象与x轴的交点的横坐标分别为-3，1，则下列结论正确的个数有（ ）