题目内容
15．
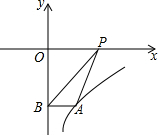如图，点A是反比例函数y=-$\frac{4}{x}$的图象上一点，过点A作AB⊥y轴于点B，点P是x轴上的一个动点，则△ABP的面积为2．
分析 设A的坐标为（a，-$\frac{4}{a}$），过A作AQ⊥OP，则三角形ABP中AB为底，AQ为高，利用三角形的面积公式求出即可．
解答 
解：设A的坐标为（a，-$\frac{4}{a}$），过A作AQ⊥OP，交OP点Q，
∴AB=a，AQ=$\frac{4}{a}$，
则S△ABP=$\frac{1}{2}$AB•AQ=$\frac{1}{2}$a•$\frac{4}{a}$=2．
故答案为：2．
点评 此题考查了反比例函数系数k的几何意义，关键是明白A的横坐标为三角形的底，A的纵坐标为底上的高．
练习册系列答案
名校课堂系列答案
相关题目
已知数轴上，点O为原点，点A对应的数为9，点B对应的数为b，点C在点B右侧，长度为2个单位的线段BC在数轴上移动．
如果所示，已知∠1=∠2，∠3=∠4，则下列结论正确的个数为（ ）
如图：△ABC是⊙O的内接三角形，AB是⊙O的直径，CD平分∠ACB交⊙O于点D，交AB于点P．连接AD、BD，AC=5，AB=10．
4．
如图所示几何体的俯视图是（ ）
如图所示几何体的俯视图是（ ）| A． |  | B． |  | C． |  | D． |  |