Question

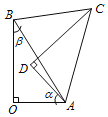
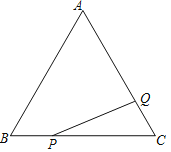
【题目】如图，已知等边△ABC的边长为4，点P，Q分别是边BC，AC上一点，PB＝1，则PA＝_____，若BQ＝AP，则AQ＝_____．

Answer 1

【答案】 3

【解析】

连接AP，过A作AD⊥BC于D，根据等边三角形的性质得到BD＝CD＝BC＝4＝2，∠BAD＝30°，根据含30°直角三角形的性质以及勾股定理可得出PA的长；连接BQ，过B作BH⊥AC于H，先根据等边三角形的性质可得出AH的长，在Rt△BHQ中，根据勾股定理可求出HQ的长，从而可得出结果．

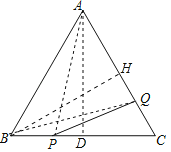
解：连接AP，过A作AD⊥BC于D，

∵△ABC是等边三角形，

∴BD＝CD＝BC＝4＝2，∠BAD＝30°，

∴BD=AB，∴AD＝AB＝2，

∵PB＝1，∴PD＝1，

∴PA＝＝＝；

连接BQ，过B作BH⊥AC于H，

∴AH＝AC＝2，

∴BH＝AD＝2，

∴HQ＝＝＝1，

∴AQ＝AH+HQ＝3，

故答案为：；3．