题目内容
5.坐标原点O到直线y=x-3的距离为$\frac{3\sqrt{2}}{2}$.分析 先求出直线y=x-3与坐标轴的交点,再利用勾股定理求出AB的长,根据三角形的面积公式即可得出结论.
解答 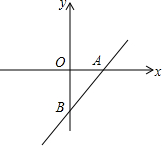 解:如图所示,
解:如图所示,
∵当x=0时,y=-3;当y=0时,x=3,
∴A(3,0),B(0,-3),
∴AB=$\sqrt{{3}^{2}+{3}^{2}}$=3$\sqrt{2}$,
∴标原点O到直线y=x-3的距离=$\frac{3×3}{3\sqrt{2}}$=$\frac{3\sqrt{2}}{2}$.
故答案为:$\frac{3\sqrt{2}}{2}$.
点评 本题考查的是一次函数图象上点的坐标特点,熟知一次函数图象上各点的坐标一定适合此函数的解析式是解答此题的关键.

练习册系列答案
相关题目
13.-2的绝对值是( )
| A. | -2 | B. | 2 | C. | -$\frac{1}{2}$ | D. | $\frac{1}{2}$ |
10.我市对城区某主干道进行绿化,计划在此公路的一侧全部栽上“市树”--樟树,要求路的两端各栽一棵,并且每两棵树的间隔相等.如果每隔5米栽1棵,则树苗缺21棵;如果每隔6米栽1棵,则树苗正好用完.设原有树苗x棵,则根据题意列出方程正确的是( )
| A. | 5(x+2)=6(x-1) | B. | 5(x+21-1)=6(x-1) | C. | 5(x+21-1)=6x | D. | 5(x+21)=6x |
14.下列四个算式中,有一个算式与其他三个算式的计算结果符号不同,则该算式是( )
| A. | (-2013)2 | B. | -20132 | C. | (-2013)3 | D. | -|-2013| |
15.下列关于二次函数y=-(x-3)2+$\frac{1}{2}$的说法,错误的是( )
| A. | 其对称轴为x=3 | B. | 其图象的顶点坐标为(3,$\frac{1}{2}$) | ||
| C. | 其图象开口方向向下 | D. | 其图象与y轴的交点坐标为(0,$\frac{1}{2}$) |