题目内容

若0°≤α≤90°，sin6α+cos6α=
14
，则α等于
 
．
分析：先把原式进行因式分解，再根据同角三角函数的关系及特殊角的三角函数值求解即可．
解答：解：∵sin6α+cos6α=
1
4
，
∴(sin2α+cos2α)•(sin4α-sin2αcos2α+cos4α)=
1
4

即1-sin2αcos22a=
1
4
，sinαcosα=
1
2
，sin2α=1，
∵0°≤α≤90°，
∴α=45°
故α答案为45°．
点评：本题考查的是特殊角的三角函数值及同角三角函数的关系，是各地中考题中常见的计算题型，需熟练掌握．
练习册系列答案
相关题目
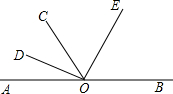精英家教网如图，O是直线AB上的点，
（1）若OD是∠AOC的平分线，OE是∠COB的平分线，求∠DOE的度数；
（2）若∠DOE=90°，OD平分∠AOC，OE是否平分∠BOC？说明理由．
24、如图1，以△ABC的边AB，AC为直角边作等腰△ABE和△ACD，M是BC的中点．
（1）若∠BAC=90°，如图1．请你猜想线段DE，AM的数量关系，并证明你的结论；
（2）若∠BAC≠90°．
①如图2．请你猜想线段DE，AM的数量关系，并证明你的结论；
②如图3．请你判断线段DE，AM的数量关系．
20、如图，Rt△ABC中，∠C=90°，将Rt△ABC绕A点旋转后，顶点B的对应点为点D
（1）请用直尺和圆规作出旋转后的△ADE；（不写作法，保留痕迹）
（2）延长BC和ED交于点F，若∠BAD=90°，说明四边形ACFE是什么四边形？
如图，正方形ABCD（四个角都是直角，四条边都相等）的边长为4，点E、F分别在边BC、CD上，且CF=1．
（1）若E为BC的中点，请你证明△AEF是直角三角形；
（2）若∠AFE=90°，求CE的值．
精英家教网
如图，已知：OB是∠AOE的平分线，OD是∠COE的平分线．
（1）若∠AOC=90°，∠COE=30°，求∠BOD的度数：
（2）若（1）中的∠COE=α（α为锐角），其它条件不变．求∠BOD的度数；
（3）若（I）中的∠AOC=β，其它条件不变．求∠BOD的度数；
（4）从（1），（2），（3）的结果中猜想∠BOD与∠AOC的数量关系是
∠BOD=
1
2
∠AOC
∠BOD=
1
2
∠AOC
．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网