题目内容
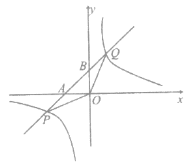
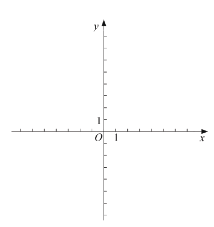
【题目】在平面直角坐标系中，过一点分别作坐标轴的垂线，若与坐标轴围成的矩形的周长与面积相等，则称这个点为“美好点”，如图，过点P分别作x轴，y轴的垂线，与坐标轴围成的矩形OAPB的周长与面积相等，则P为“美好点”．
（1）在点M（2，2），N（4，4），Q（﹣6，3）中，是“美好点”的有 ；
（2）若“美好点”P（a，﹣3）在直线y＝x+b（b为常数）上，求a和b的值；
（3）若“美好点”P恰好在抛物线y＝
x2第一象限的图象上，在x轴上是否存在一点Q使得△POQ为直角三角形？若存在，请求出点Q的坐标；若不存在，请说明理由．
【答案】（1）N、Q；（2）a＝6，b＝﹣9或a＝﹣6，b＝3；（3）存在，点Q的坐标为（6，0）或（
，0）．
【解析】
（1）根据“美好点”的定义逐个验证即可；
（2）对于P点，对应图形的周长为：2×（|a|+3）=2|a|+6，面积为3|a|，因为点P是“美好点”，故2|a|+6=3|a|，即可求解；
（3）根据点P是“美好点”确定点P的坐标，设点Q的坐标为（x，0），再分以下三种情况：当∠POQ=90°时，此种情况不存在；当∠PQO=90°时，则PO2=PQ2+OQ2；当∠OPQ=90°时，则OQ2=PQ2+OP2，分别列出关于x的方程，解得x即可．
解：（1）对于M点，对应图形的周长为：2×（2+2）＝8，面积为2×2＝4≠8，故点M不是“美好点”；
对于点N，对应图形的周长为：2×（4+4）＝16，面积为4×4＝16，故点N是“美好点”；
对于点Q，对应图形的周长为：2×（6+3）＝18，面积为6×3＝18，故点Q是“美好点”；
故答案为：N、Q；
（2）对于P点，对应图形的周长为2×（|a|+3）＝2|a|+6，面积为3|a|，
∵点P是“美好点”，
∴2|a|+6＝3|a|，解得：a＝±6，
将P（a，﹣3）代入y＝x+b得：﹣3＝a+b，则b＝﹣3﹣a，
∴当a=6时，b=-9；当a=-6时，b=3，
故a＝6，b＝﹣9或a＝﹣6，b＝3；
（3）存在，理由如下：
设点P的坐标为（m，n），则n＝
m2（m＞0，n＞0），
由题意得：2m+2n＝mn，∴2m+
m2＝m3，
解得：m＝6或﹣4（舍去）或0（舍去），
故点P的坐标为（6，3）；
设点Q的坐标为（x，0），
则PQ2＝（x﹣6）2+32＝（x﹣6）2+9，
PO2＝36+9＝45，
OQ2＝x2，
当∠POQ=90°时，∵点Q在x轴上，则∠POQ≠90°，此种情况不存在；
当∠PQO=90°时，则PO2=PQ2+OQ2，∴45=（x﹣6）2+9+ x2，解得x＝6或x=0（舍去）；
当∠OPQ=90°时，则OQ2=PQ2+OP2，∴x2=（x﹣6）2+9+45，解得x＝；
综上所述，符合条件的点Q的坐标为：（6，0）或（，0）．
