题目内容
 如图,四边形ABCD放在了一组距离相等的平行线中,已知BD=6cm,四边形ABCD的面积为24cm,则两条平行线间的距离为( )
如图,四边形ABCD放在了一组距离相等的平行线中,已知BD=6cm,四边形ABCD的面积为24cm,则两条平行线间的距离为( )| A、2 | B、3 | C、4 | D、1 |
考点:平行线之间的距离,三角形的面积
专题:
分析:根据面积的和差,可得S四边形ABCD=S△ABD+S△BCD,根据平行线间的距离相等,可得AE与CF的关系,根据解方程,可得答案.
解答:解:如图:

作AE⊥BD,CF⊥BD,
由面积的和差,BD=6cm,得
S四边形ABCD=S△ABD+S△BCD=
BD•AE+
BD•CF=
BD•3CF+
BD•CF=24.
解得CD=2,
故选:A.

作AE⊥BD,CF⊥BD,
由面积的和差,BD=6cm,得
S四边形ABCD=S△ABD+S△BCD=
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
解得CD=2,
故选:A.
点评:本题考查了平行线间的距离,利用了平行线间的距离相等,面积的和差.

练习册系列答案
 口算题卡加应用题集训系列答案
口算题卡加应用题集训系列答案
相关题目
 根据生物学研究结果,青春期男女生身高增长速度呈现如图规律,由图可以判断,下列说法错误的是( )
根据生物学研究结果,青春期男女生身高增长速度呈现如图规律,由图可以判断,下列说法错误的是( )| A、男生在13岁时身高增长速度最快 |
| B、女生在10岁以后身高增长速度放慢 |
| C、11岁时男女生身高增长速度基本相同 |
| D、9-10岁时女生身高比男生身高要高 |
二次函数y=(x-2)2-3的图象上最低点的坐标是( )
| A、(-2,-3) |
| B、(2,-3) |
| C、(-2,3) |
| D、(2,3) |

 如图,为了测量一栋楼的高度,王青同学在她脚下放了一面镜子,然后向后退,直到她刚好在镜子中看到大楼顶部.这时∠LMK等于∠SMT吗?如果王青身高1.55m,她估计自己眼睛离地面1.50m,同时量得LM=0.30m,MS=25m,这栋大楼有多高?
如图,为了测量一栋楼的高度,王青同学在她脚下放了一面镜子,然后向后退,直到她刚好在镜子中看到大楼顶部.这时∠LMK等于∠SMT吗?如果王青身高1.55m,她估计自己眼睛离地面1.50m,同时量得LM=0.30m,MS=25m,这栋大楼有多高? 如图,⊙O的直径是4cm,C是
如图,⊙O的直径是4cm,C是
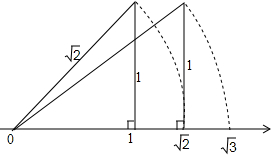 如图,由勾股定理:两条直角边长都为1的直角三角形,其斜边长为
如图,由勾股定理:两条直角边长都为1的直角三角形,其斜边长为