��Ŀ����
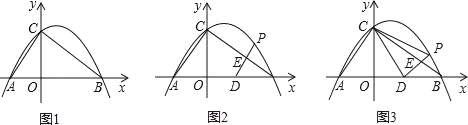
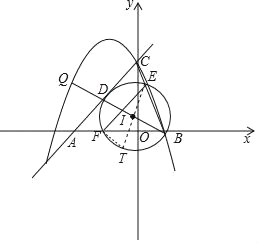
����Ŀ����ͼ1��ֱ��l��y=x+![]() ��x�Ḻ���ᡢy��������ֱ��ཻ��A��C���㣬������y=��
��x�Ḻ���ᡢy��������ֱ��ཻ��A��C���㣬������y=��![]() x2+bx+c������B��1��0���͵�C��
x2+bx+c������B��1��0���͵�C��

��1���������ߵĽ���ʽ��
��2����֪��Q��������y=��![]() x2+bx+c�ڵڶ������ڵ�һ�����㣮
x2+bx+c�ڵڶ������ڵ�һ�����㣮
����ͼ1������AQ��CQ�����Q�ĺ�����Ϊt����AQC�����ΪS����S��t�ĺ�����ϵʽ�������S�����ֵ��
������BQ��AC�ڵ�D������BC����BDΪֱ������I���ֱ�BC��AB�ڵ�E��F������EF�����߶�EF����Сֵ����ֱ��д����ʱ��Q�����꣮
���𰸡���1��y=��![]() x2��
x2��![]() x+
x+![]() ����2����S=��
����2����S=��![]() t2��
t2��![]() t����3��t��0��,
t����3��t��0��,![]() ����EF=
����EF=![]() ����Q��������
����Q��������![]() ��3��4��
��3��4��![]() ����
����
��������
������1������ֱ�ߵĽ���ʽ�õ���![]() �ѵ�B(1,0)���
�ѵ�B(1,0)���![]() ����
����![]() ���ǵõ����ۣ�
���ǵõ����ۣ�
��2��������OQ,��ֱ��![]() ��,��y=0,��
��,��y=0,��![]() �õ���
�õ���![]() ���������ε������ʽ���ɵõ����ۣ�
���������ε������ʽ���ɵõ����ۣ�
�ڽ�ֱ�������εõ�![]() ��ֱ��ET����I�ڵ�T,����FT,��
��ֱ��ET����I�ڵ�T,����FT,��![]()
�õ�![]() ��BD��ACʱ����ʱֱ��BD��С����ֱ��ET��С��EF��ֵ��С���Ƴ�
��BD��ACʱ����ʱֱ��BD��С����ֱ��ET��С��EF��ֵ��С���Ƴ�![]() ��Rt��ADB�У��������Ǻ����Ķ��弴�ɵõ����ۣ�
��Rt��ADB�У��������Ǻ����Ķ��弴�ɵõ����ۣ�
���������(1)��ֱ��![]() ��,��x=0,��
��,��x=0,��![]()
���![]()
�ѵ�B(1,0)���![]() ����
����![]() �ã�
�ã�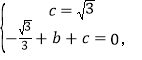
��ã�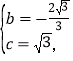
�������ߵĽ���ʽΪ��![]()
(2)������OQ,��ֱ��![]() ��,��y=0,��
��,��y=0,��![]()
���![]()
![]()
![]()
![]() ��
��![]()
�൱![]() ʱ,S���ֵ
ʱ,S���ֵ![]()
�ڡߵ�B(1,0), ![]()
![]()
��Rt��BOC��, ![]()
![]()
��ֱ��ET����I�ڵ�T,����FT,��![]()
��![]()
��BD��ACʱ����ʱֱ��BD��С����ֱ��ET��С��EF��ֵ��С��
��Rt��AOC��, ![]()
![]()
��Rt��ADB����![]()
![]()
��ʱ��Q������Ϊ![]()

 ����������������ϵ�д�
����������������ϵ�д�