题目内容
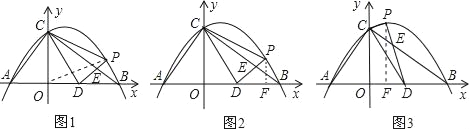
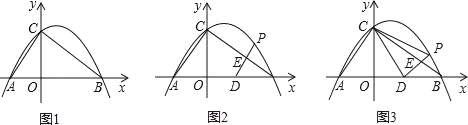
【题目】已知：Rt△ABC的斜边长为5，斜边上的高为2，将这个直角三角形放置在平面直角坐标系中，使其斜边AB与x轴重合（其中OA＜OB），直角顶点C落在y轴正半轴上（如图1）．
（1）求线段OA、OB的长和经过点A、B、C的抛物线的关系式．
（2）如图2，点D的坐标为（2，0），点P（m，n）是该抛物线上的一个动点（其中m＞0，n＞0），连接DP交BC于点E．
①当△BDE是等腰三角形时，直接写出此时点E的坐标．
②又连接CD、CP（如图3），△CDP是否有最大面积？若有，求出△CDP的最大面积和此时点P的坐标；若没有，请说明理由．
【答案】（1）
（2）①（3，
），（
，
），（
，
）②当m=
时，△CDP的面积最大．此时P点的坐标为（，
），S△CDP的最大值是
【解析】试题（1）由Rt△ABC中，CO⊥AB可证△AOC∽△COB，由相似比得OC2=OAOB，设OA的长为x，则OB=5-x，代入可求OA，OB的长，确定A，B，C三点坐标，求抛物线解析式；
（2）根据△BDE为等腰三角形，分为DE=EB，EB=BD，DE=BD三种情况，分别求E点坐标；
（3）作辅助线，将求△CDP的面积问题转化．方法一：如图1，连接OP，根据S△CDP=S四边形CODP-S△COD=S△COP+S△ODP-S△COD，表示△CDP的面积；方法二：过点P作PE⊥x轴于点F，则S△CDP=S梯形COFP-S△COD-S△DFP，表示△CDP的面积；再利用二次函数的性质求出△CDP的最大面积和此时点P的坐标．
试题解析：
（1）设OA的长为x，则OB=5﹣x；
∵OC=2，AB=5，∠BOC=∠AOC=90°，∠OAC=∠OCB；
∴△AOC∽△COB，∴OC2=OAOB
∴22=x（5﹣x）
解得：x1=1，x2=4，
∵OA＜OB，∴OA=1，OB=4；
∴点A、B、C的坐标分别是：A（﹣1，0），B（4，0），C（0，2）；
方法一：设经过点A、B、C的抛物线的关系式为：y=ax2+bx+2，
将A、B、C三点的坐标代入得
…
解得：a=
，
所以这个二次函数的表达式为：y=
方法二：设过点A、B、C的抛物线的关系式为：y=a（x+1）（x﹣4）…
将C点的坐标代入得：a=-
所以这个二次函数的表达式为：y=
（2）①当△BDE是等腰三角形时，点E的坐标分别是：(3,),(
，(4-
) ．
②如图1，连接OP，
S△CDP=S四边形CODP﹣S△COD=S△COP+S△ODP﹣S△COD
=
img src="https://thumb.zyjl.cn/Upload/2019/04/15/10/a0e4069c/SYS201904151009117939279132_DA/SYS201904151009117939279132_DA.016.png" width="218" height="37" style="-aw-left-pos:0pt; -aw-rel-hpos:column; -aw-rel-vpos:paragraph; -aw-top-pos:0pt; -aw-wrap-type:inline" />
∴当m=时，△CDP的面积最大．此时P点的坐标为（， ），
S△CDP的最大值是．
另解：如图2、图3，过点P作PF⊥x轴于点F，则
S△CDP=S梯形COFP﹣S△COD﹣S△DFP
=
∴当m=时，△CDP的面积最大．此时P点的坐标为（， ），
S△CDP的最大值是．
