题目内容
 已知:如图,在平行四边形ABCD中,BE、CE分别平分∠ABC、∠BCD,E在AD上,BE=12cm,CE=5cm.
已知:如图,在平行四边形ABCD中,BE、CE分别平分∠ABC、∠BCD,E在AD上,BE=12cm,CE=5cm.
则:(1)平行四边形ABCD的周长=________;
(2)平行四边形ABCD的面积=________.
解:(1)∵BE和CE分别平分∠ABC和∠BCD,
∵AB∥CD,
∴∠ABC+∠DCB=180°,
∴ (∠ABC+∠DCB)=90°,
(∠ABC+∠DCB)=90°,
BE和CE分别是∠ABC和∠BCD平分线,
∴∠EBC+∠ECB=90°,
△EBC是直角三角形,
根据勾股定理:BC=13,
∵AD∥BC,
∠DEC=∠ECB,(内错角相等)
∠ECD=∠ECB,(已知)
∴∠DEC=∠ECD,
DE=CD,
同理AB=AE,
AB+CD=AE+DE=AD=BC=13,
∴平行四边形ABCD周长=BC+AD+AB+CD=13+13+13=39,
故答案为:39.
(2)如图,作EH⊥BC,垂足为H
 S△BEC=
S△BEC= BE×EC=
BE×EC= ×12×5=30,
×12×5=30,
S△BEC= ×BC×EH=13×EH×
×BC×EH=13×EH× ,
,
13×EH× =30,
=30,
EH= ,
,
∴S平行四边形ABCD=BC*EH=13× =60,
=60,
故答案为:60.
分析:(1)根据平行线的性质和角平分线的性质求出∠EBC+∠ECB=90°,推出△EBC是直角三角形,根据勾股定理求出BC,根据等腰三角形的判定推出DE=CD,AB=AE,即可求出平行四边形的周长;
(2)作EH⊥BC,垂足H,根据三角形的面积公式求出DH,根据面积求出即可.
点评:本题主要考查对平行四边形的性质,等腰三角形的性质和判定,勾股定理,勾股定理的逆定理,平行线的性质,角平分线的性质,三角形的面积等知识点的理解和掌握,能综合运用这些性质进行推理是解此题的关键.
∵AB∥CD,
∴∠ABC+∠DCB=180°,
∴
 (∠ABC+∠DCB)=90°,
(∠ABC+∠DCB)=90°,BE和CE分别是∠ABC和∠BCD平分线,
∴∠EBC+∠ECB=90°,
△EBC是直角三角形,
根据勾股定理:BC=13,
∵AD∥BC,
∠DEC=∠ECB,(内错角相等)
∠ECD=∠ECB,(已知)
∴∠DEC=∠ECD,
DE=CD,
同理AB=AE,
AB+CD=AE+DE=AD=BC=13,
∴平行四边形ABCD周长=BC+AD+AB+CD=13+13+13=39,
故答案为:39.
(2)如图,作EH⊥BC,垂足为H
 S△BEC=
S△BEC= BE×EC=
BE×EC= ×12×5=30,
×12×5=30,S△BEC=
 ×BC×EH=13×EH×
×BC×EH=13×EH× ,
,13×EH×
 =30,
=30,EH=
 ,
,∴S平行四边形ABCD=BC*EH=13×
 =60,
=60,故答案为:60.
分析:(1)根据平行线的性质和角平分线的性质求出∠EBC+∠ECB=90°,推出△EBC是直角三角形,根据勾股定理求出BC,根据等腰三角形的判定推出DE=CD,AB=AE,即可求出平行四边形的周长;
(2)作EH⊥BC,垂足H,根据三角形的面积公式求出DH,根据面积求出即可.
点评:本题主要考查对平行四边形的性质,等腰三角形的性质和判定,勾股定理,勾股定理的逆定理,平行线的性质,角平分线的性质,三角形的面积等知识点的理解和掌握,能综合运用这些性质进行推理是解此题的关键.

练习册系列答案
相关题目
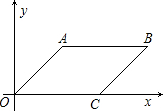 如图,在平行四边形ABC0中,已知点A、C两点的坐标为A(
如图,在平行四边形ABC0中,已知点A、C两点的坐标为A(
 (2013•南平模拟)如图,已知四边形ABCD.请在下列四个关系中,选出两个恰当的关系作为条件,推出四边形ABCD是平行四边形,并予证明.
(2013•南平模拟)如图,已知四边形ABCD.请在下列四个关系中,选出两个恰当的关系作为条件,推出四边形ABCD是平行四边形,并予证明. 如图,在平行四边形OABC中,已知点A、C两点的坐标为A (
如图,在平行四边形OABC中,已知点A、C两点的坐标为A (