题目内容
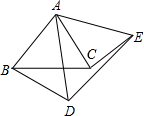已知△ABC和△ADE是等边三角形，求证：BD=CE．
证明：∵△ABC和△ADE是等边三角形，
∴AB=AC，AD=AE，∠BAC=∠DAE=60°，
∴∠BAC-∠DAC=∠DAE-∠DAC，
即∠BAD=∠CAE，
∴在△ABD和△ACE中
∴△ABD≌△ACE，
∴BD=CE．
分析：根据等边三角形性质得出AB=AC，AD=AE，∠BAC=∠DAE=60°，求出∠BAD=∠CAE，证出△ABD≌△ACE即可．
点评：本题考查了等边三角形性质和全等三角形的性质和判定的应用，关键是推出△ABD≌△ACE．
∴AB=AC，AD=AE，∠BAC=∠DAE=60°，
∴∠BAC-∠DAC=∠DAE-∠DAC，
即∠BAD=∠CAE，
∴在△ABD和△ACE中
∴△ABD≌△ACE，
∴BD=CE．
分析：根据等边三角形性质得出AB=AC，AD=AE，∠BAC=∠DAE=60°，求出∠BAD=∠CAE，证出△ABD≌△ACE即可．
点评：本题考查了等边三角形性质和全等三角形的性质和判定的应用，关键是推出△ABD≌△ACE．
练习册系列答案
中考解读考点精练系列答案
相关题目
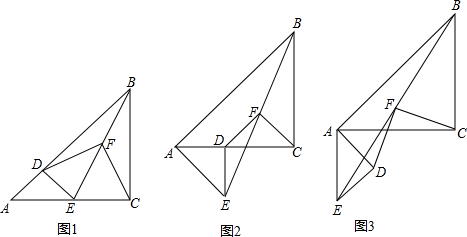
（2012•南岗区二模）如图，已知△ABC和△DBE均为等腰直角三角形，∠ABC=∠DBE=90°，求证：AD=CE．
如图，已知△ABC和△BAD中，AC=DB，若不增加任何字母与辅助线，要证明△ABC≌△BAD；则还需要增加一个条件是