题目内容
【题目】问题情境:有一堵长为![]() 的墙,利用这堵墙和长为
的墙,利用这堵墙和长为![]() 的篱笆围成一个矩形养鸡场,怎样围面积最大?最大面积是多少?
的篱笆围成一个矩形养鸡场,怎样围面积最大?最大面积是多少?
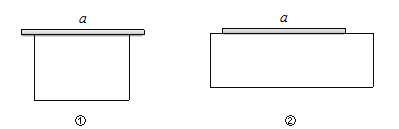
题意理解:根据题意,有两种设计方案:一边靠墙(如图①)和一边“包含”墙(如图②).
特例分析:
(1)当![]() 时,若按图①的方案设计,则该方案中养鸡场的最大面积是
时,若按图①的方案设计,则该方案中养鸡场的最大面积是 ![]() ;若按图②的方案设计,则该方案中养鸡场的最大面积是
;若按图②的方案设计,则该方案中养鸡场的最大面积是 ![]() .
.
(2)当![]() 时,解决“问题情境”中的问题.
时,解决“问题情境”中的问题.
解决问题:(3)直接写出“问题情境”中的问题的答案.
【答案】(1)288,324;(2)当![]() 时,该养鸡场围成一个边长为
时,该养鸡场围成一个边长为![]() 的正方形时面积最大,最大面积是
的正方形时面积最大,最大面积是![]() ;(3)当
;(3)当![]() 时,当矩形的长为
时,当矩形的长为![]() ,宽为
,宽为![]() 时,养鸡场最大面积为
时,养鸡场最大面积为![]()
【解析】
(1)根据a=12,分类讨论即可,见详解,(2)表示出![]() ,根据二次函数的性质即可解题,(3)根据养鸡场的一边靠墙或包含墙分类讨论,再利用二次函数的性质求出最值即可解题.
,根据二次函数的性质即可解题,(3)根据养鸡场的一边靠墙或包含墙分类讨论,再利用二次函数的性质求出最值即可解题.
解:(1)如图①,设矩形的长为x米,则矩形的宽为(30-![]() )米,面积为S,依题意得:
)米,面积为S,依题意得:
S=x·(30-![]() )=-
)=-![]() =-
=-![]() ,(x
,(x![]() 12)
12)
∴当x=12时,矩形有最大值为288![]()
如图②, 设矩形的长为x米, 则矩形的宽为(36-x)米,依题意得:
S=x·(36-x)=-![]() ,
,
∴当x=18时,矩形有最大值为324![]()
综上,矩形的面积为288,324.
(2)如图①,设![]() ,则
,则![]() .
.
所以![]() .
.

根据题意,得![]() .
.
因为![]() ,
,
所以当![]() 时,
时,![]() 随
随![]() 的增大而减小.
的增大而减小.
即当![]() 时,
时,![]() 有最大值,最大值是400(m2).
有最大值,最大值是400(m2).
如图②,设![]() ,则
,则![]() .
.
所以![]() .
.

根据题意,得![]() .
.
因为![]() ,
,
所以当![]() 时,
时,
![]() 有最大值,最大值是
有最大值,最大值是![]() .
.
综上,当![]() 时,该养鸡场围成一个边长为
时,该养鸡场围成一个边长为![]() 的正方形时面积最大,最大面积是
的正方形时面积最大,最大面积是![]() .
.
(3)当![]() 时,围成边长为
时,围成边长为![]() 的正方形面积最大,最大面积是
的正方形面积最大,最大面积是![]() .
.
当![]() 时,围成两邻边长分别为
时,围成两邻边长分别为![]() ,
,![]() 的养鸡场面积最大,最大面积为
的养鸡场面积最大,最大面积为![]() .
.
当![]() 时,当矩形的长为
时,当矩形的长为![]() ,宽为
,宽为![]() 时,养鸡场最大面积为
时,养鸡场最大面积为![]() .
.

【题目】为了让同学们了解自己的体育水平,初二1班的体育刘老师对全班45名学生进行了一次体育模拟测试(得分均为整数),成绩满分为10分,1班的体育委员根据这次测试成绩,制作了统计图和分析表如下:
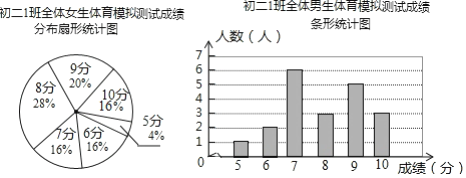
初二1班体育模拟测试成绩分析表
平均分 | 方差 | 中位数 | 众数 | |
男生 | ________ | 2 | 8 | 7 |
女生 | 7.92 | 1.99 | 8 | ________ |
根据以上信息,解答下列问题:
(1)这个班共有男生________人,共有女生________人;
(2)补全初二1班体育模拟测试成绩分析表;
(3)你认为在这次体育测试中,1班的男生队、女生队哪个表现更突出一些?并写出一条支持你的看法的理由.