题目内容
8.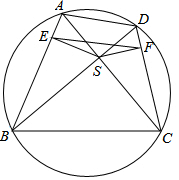 如图所示,圆的内接四边形ABCD的两条对角线AC、BD的交点为S,S在边AB、CD上的投影分别为E、F.证明EF的中垂线平分线段AD、BC.
如图所示,圆的内接四边形ABCD的两条对角线AC、BD的交点为S,S在边AB、CD上的投影分别为E、F.证明EF的中垂线平分线段AD、BC.
分析 先判断出△BES∽△CFS得出BS•FS=CS•ES,∠CSE=∠BSF,即可得出BS•FS•cos∠BSF=CS•ES•cos∠CSE,再根据余弦定理得,BS2+FS2-BF2=CS2+ES2-EC2,即:BS2-ES2+EC2=CS2-FS2+BF2,再根据勾股定理得出结论结合前面的式子得出BE2+EC2=CF2+BF2①,最后用勾股定理和中点即可得出EB2+EC2=2(EM2+BM2)④,同样的办法得出
FB2+FC2=2(FM2+BM2)⑤,结合①④⑤即可判断出EF的中垂线平分线段BC,即可得出结论.
解答 解:如图, 连接BF,CE,
连接BF,CE,
∵S在边AB、CD上的投影分别为E、F,
∴∠BES=∠CFS=90°,
∵∠EBS=∠FCS,
∴△BES∽△CFS,
∴∠BSE=∠CSF,
∴∠CSE=∠BSF,
∵△BES∽△CFS,
∴∠$\frac{BS}{CS}=\frac{ES}{FS}$,
∴BS•FS=CS•ES,
∴BS•FS•cos∠BSF=CS•ES•cos∠CSE,
根据余弦定理得,BS2+FS2-BF2=CS2+ES2-EC2,
∴BS2-ES2+EC2=CS2-FS2+BF2,
在Rt△BES中,BS2-ES2=BE2,
在Rt△CFS中,CS2-FS2=CF2,
∴BE2+EC2=CF2+BF2①,
取BC的中点M,连接EM,FM
∴BM=CM,
作EH⊥BC于H,
∴BH=BM-HM,
在Rt△EMH中,EM2=EH2+MH2,
在Rt△EBH中,EB2=EH2+BH2=EH2+(BM-HM)2=EH2+BM2+HM2-2BM•HM+HM2,
∴EB2=EM2+BM2-2BM•HM=EM2+CM2-2CM•HM②,
同理:EC2=EM2+CM2+2CM•HM③,
②+③得,EB2+EC2=2EM2+2CM2=2(EM2+CM2)=2(EM2+BM2)④,
同理:FB2+FC2=2(FM2+BM2)⑤,
由①④⑤得,2(EM2+BM2)=2(FM2+BM2),
∴EM=FM,
∴△EMF是等腰三角形,
∵点M是BC的中点,
∴点M是EF的垂直平分线上,
∴EF的中垂线平分线段BC.
同理:EF的中垂线平分线段AD.
即:EF的中垂线平分线段AD、BC.
点评 此题是圆的综合题.主要考查了相似三角形的判定和性质,余弦定理,勾股定理,等腰三角形的判定和性质,解本题的关键是EB2+EC2=2(EM2+BM2)和FB2+FC2=2(FM2+BM2),也是解本题的难点,是一道难度比较大的竞赛题.

 阅读快车系列答案
阅读快车系列答案| A. | x=2 | B. | x=-2 | C. | x1=1,x2=4 | D. | x1=2,x2=-2 |
| A. | 1004<a<1005 | B. | 1004≤a<1005 | ||
| C. | 1004<a<1005或-1005≤a<-1004 | D. | 1004≤a<1005或-1005<a≤-1004 |
| A. | 恢复原价 | B. | 降价4% | C. | 提价4% | D. | 以上都不对 |
| A. | 正整数和正分数统称正有理数 | B. | 两个无理数相乘的结果可能等于零 | ||
| C. | 正整数,0,负整数统称为整数 | D. | 3.1415926是小数,也是分数 |
 如图,在长和宽分别为m,n的长方形铁皮的四个角都剪去一个边长为x的正方形(2x<n<m),折叠后,做成一无盖的盒子,则这个长方体盒子的表面积是mn-4x2.
如图,在长和宽分别为m,n的长方形铁皮的四个角都剪去一个边长为x的正方形(2x<n<m),折叠后,做成一无盖的盒子,则这个长方体盒子的表面积是mn-4x2. 把下列各数填在相应的圆圈集合内:
把下列各数填在相应的圆圈集合内: