题目内容
一名投递员开着装满油的摩托车沿东西方向进行投递,早晨从A地出发,中午到达B地,约定向东为正方向.整个上午的行程依次记录如下(单位:千米):7,-5,9,-4,6,-3,5,-2.
(1)求B地在A地的什么位置?
(2)求上午行程中离A地最远的位置.
(3)若摩托车耗油a升/千米,油箱容量为15a升,途中需补充多少升油?
(1)求B地在A地的什么位置?
(2)求上午行程中离A地最远的位置.
(3)若摩托车耗油a升/千米,油箱容量为15a升,途中需补充多少升油?
考点:正数和负数
专题:
分析:(1)根据有理数的加法,可得答案;
(2)根据有理数的加法,可得每次与出发地的距离,根据有理数的大小比较,可得答案;
(3)根据行车路程乘以单位耗油量,可得答案.
(2)根据有理数的加法,可得每次与出发地的距离,根据有理数的大小比较,可得答案;
(3)根据行车路程乘以单位耗油量,可得答案.
解答:解:(1)7-5+9-4++6-3+5-2=13(千米).
答:B地在A地东15千米;
(2)7-5=2,2+9=11,11-4=7,7+6=13,13-3=10,10+5=15,15-2=13,
15>13>11>7>2.
答:上午行程中离A地最远的位置东15千米;
(3)(7+|-5|+9+|-4|+6+|-3|+5+|-2|)a=41a(升),
41a-15a=26a(升).
答:途中需补充26升油.
答:B地在A地东15千米;
(2)7-5=2,2+9=11,11-4=7,7+6=13,13-3=10,10+5=15,15-2=13,
15>13>11>7>2.
答:上午行程中离A地最远的位置东15千米;
(3)(7+|-5|+9+|-4|+6+|-3|+5+|-2|)a=41a(升),
41a-15a=26a(升).
答:途中需补充26升油.
点评:本题考查了正数和负数,利用了有理数的加法运算,行车路程乘以单位耗油量.

练习册系列答案
 探究与巩固河南科学技术出版社系列答案
探究与巩固河南科学技术出版社系列答案
相关题目
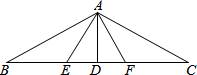 如图,在△ABC中,AB=AC,AE=AF,AD⊥BC于点D,且点E、F在BC上,则图中全等的直角三角形共有( )
如图,在△ABC中,AB=AC,AE=AF,AD⊥BC于点D,且点E、F在BC上,则图中全等的直角三角形共有( )| A、1对 | B、2对 | C、3对 | D、4对 |
已知k>0,则一次函数y=kx-k的图象大致是( )
A、 |
B、 |
C、 |
D、 |
小明想做一个直角三角形的木架,以下四组木棒中,哪一组的三条能够刚好做成( )
| A、12,15,17 | ||||
B、
| ||||
| C、7,12,15 | ||||
D、3,4,
|
 如图是二次函数y=ax2+bx+c的部分图象,其中与x轴的一个交点坐标是(5,0),对称轴是直线x=2,则它与x轴的另一个交点坐标为
如图是二次函数y=ax2+bx+c的部分图象,其中与x轴的一个交点坐标是(5,0),对称轴是直线x=2,则它与x轴的另一个交点坐标为