题目内容
已知正比例函数y=-kx和一次函数y=kx-2（x为自变量），它们在同一坐标系内的图象大致是
- A.
- B.
- C.
- D.
A
分析：分k大于0和k小于0两种情况讨论．k＞0时，分别画出两函数图象；k＜0时分别画出两函数图象；与选项中图象对照．符合题意的即为正确答案．
解答：分两种情况：（1）当k＞0时，正比例函数y=-kx的图象过原点、第一、三象限，一次函数y=kx-2的图象经过第一、三、四象限，选项A符合；
（2）当k＜0时，正比例函数y=-kx的图象过原点、第二、四象限，一次函数y=kx-2的图象经过第二、三、四象限，无选项符合．
故选A．
点评：一次函数y=kx+b的图象有四种情况：
①当k＞0，b＞0，函数y=kx+b的图象经过第一、二、三象限；
②当k＞0，b＜0，函数y=kx+b的图象经过第一、三、四象限；
③当k＜0，b＞0时，函数y=kx+b的图象经过第一、二、四象限；
④当k＜0，b＜0时，函数y=kx+b的图象经过第二、三、四象限．
分析：分k大于0和k小于0两种情况讨论．k＞0时，分别画出两函数图象；k＜0时分别画出两函数图象；与选项中图象对照．符合题意的即为正确答案．
解答：分两种情况：（1）当k＞0时，正比例函数y=-kx的图象过原点、第一、三象限，一次函数y=kx-2的图象经过第一、三、四象限，选项A符合；
（2）当k＜0时，正比例函数y=-kx的图象过原点、第二、四象限，一次函数y=kx-2的图象经过第二、三、四象限，无选项符合．
故选A．
点评：一次函数y=kx+b的图象有四种情况：
①当k＞0，b＞0，函数y=kx+b的图象经过第一、二、三象限；
②当k＞0，b＜0，函数y=kx+b的图象经过第一、三、四象限；
③当k＜0，b＞0时，函数y=kx+b的图象经过第一、二、四象限；
④当k＜0，b＜0时，函数y=kx+b的图象经过第二、三、四象限．
练习册系列答案
天天向上一本好卷系列答案
小学生10分钟应用题系列答案
相关题目
已知正比例函数y=k1x（k1≠0）与反比例函数y=
（k2≠0）的图象有一个交点的坐标为（-2，-1），则它的另一个交点的坐标是（ ）
| k2 |
| x |
| A、（2，1） |
| B、（-2，-1） |
| C、（-2，1） |
| D、（2，-1） |
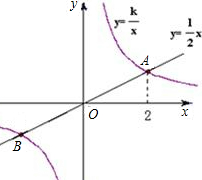横坐标为2．
如图，已知正比例函数和反比例函数的图象都经过点A（3，3）．