题目内容
11.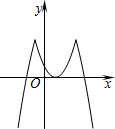 如图,将抛物线y=(x-1)2 的图象位于直线y=4以上的部分向下翻折,得到新的图象(实线部分),若直线y=-x+m与新图象只有四个交点,求m的取值范围.( )
如图,将抛物线y=(x-1)2 的图象位于直线y=4以上的部分向下翻折,得到新的图象(实线部分),若直线y=-x+m与新图象只有四个交点,求m的取值范围.( )| A. | $\frac{3}{4}$<m<3 | B. | $\frac{3}{4}$<m<7 | C. | $\frac{4}{3}$<m<7 | D. | $\frac{4}{3}$<m<3 |
分析 根据函数图象,可发现,若直线与新函数有3个交点,可以有两种情况:
①直线经过点A(即左边的对折点),可将A点坐标代入直线的解析式中,即可求出m的值;
②若直线与新函数图象有三个交点,那么当直线与该二次函数只有一个交点时,恰好满足这一条件,那么联立直线与该二次函数的解析式,可化为一个关于x的一元二次方程,那么该方程的判别式△=0,根据这一条件可确定m的取值.
解答 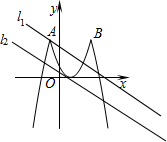 解:令y=4,则4=(x-1)2,
解:令y=4,则4=(x-1)2,
解得x=3或-1,
∴A(-1,4),
平移直线y=-x+m知:直线位于l1和l2时,它与新图象有三个不同的公共点.
①当直线位于l1时,此时l1过点A(-1,4),
∴4=1+m,即m=3.
②当直线位于l2时,此时l2与函数y=(x-1)2 的图象有一个公共点,
∴方程-x+m=x2-2x+1,
即x2-x+1-m=0有两个相等实根,
∴△=1-4(1-m)=0,
即m=$\frac{3}{4}$.
由①②知若直线y=-x+m与新图象只有四个交点,m的取值范围为$\frac{3}{4}$<m<3;
故选A.
点评 此题考查了二次函数图象与几何变换、一次函数的性质、函数图象交点以及根据值域确定二次函数参数取值范围的问题,综合性强,难度较大.

练习册系列答案
 金钥匙试卷系列答案
金钥匙试卷系列答案
相关题目
2.下列说法正确的是( )
①0是绝对值最小的实数;
②相反数大于本身的数是负数;
③数轴上原点两侧的数互为相反数;
④带根号的数是无理数.
①0是绝对值最小的实数;
②相反数大于本身的数是负数;
③数轴上原点两侧的数互为相反数;
④带根号的数是无理数.
| A. | ①② | B. | ①③ | C. | ①②③ | D. | ①②③④ |
6.计算9÷(-3)的结果等于( )
| A. | -3 | B. | 3 | C. | $\frac{1}{3}$ | D. | -$\frac{1}{3}$ |
16.《九章算术》是中国古代的数学专著,下面这道题是《九章算术》中第七章的一道题:“今有共买物,人出八,盈三;人出七,不足四,问人数、物价各几何?”译文:“几个人一起去购买某物品,如果每人出8钱,则多了3钱;如果每人出7钱,则少了4钱.问有多少人,物品的价格是多少?”设有x人,物品价格为y钱,可列方程组为( )
| A. | $\left\{{\begin{array}{l}{8x-3=y}\\{7x+4=y}\end{array}}\right.$ | B. | $\left\{{\begin{array}{l}{8x+3=y}\\{7x-4=y}\end{array}}\right.$ | C. | $\left\{{\begin{array}{l}{y-8x=3}\\{y-7x=4}\end{array}}\right.$ | D. | $\left\{{\begin{array}{l}{8x-y=3}\\{7x-y=4}\end{array}}\right.$ |
1.下列图形:

任取一个是中心对称图形的概率是( )

任取一个是中心对称图形的概率是( )
| A. | $\frac{1}{4}$ | B. | $\frac{1}{2}$ | C. | $\frac{3}{4}$ | D. | 1 |
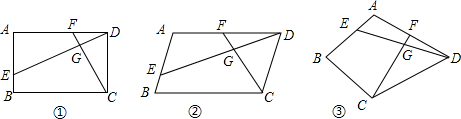 已知四边形ABCD中,E、F分别是AB、AD边上的点,DE与CF交于点G.
已知四边形ABCD中,E、F分别是AB、AD边上的点,DE与CF交于点G.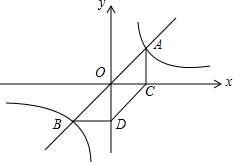 如图,一过原点的直线y=mx(m>0)与反比例函数$y=\frac{k}{x}$(k>0)的图象交于A、B两点,过A、B两点分别向x轴、y轴作垂线,垂足分别为C、D两点,连接CD.
如图,一过原点的直线y=mx(m>0)与反比例函数$y=\frac{k}{x}$(k>0)的图象交于A、B两点,过A、B两点分别向x轴、y轴作垂线,垂足分别为C、D两点,连接CD.