题目内容

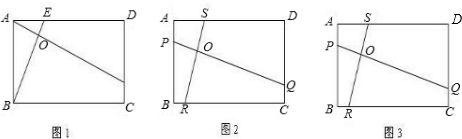
如图，点M、N都在反比例函数的图象上，则△OMN的面积为
3
2
3
2
．
分析：如图，过点M、N作MC，ND分别垂直于x轴，易得△OMN的面积为梯形CDNM的面积．
解答：解：如图，过点M、N作MC，ND分别垂直于x轴．
∵点M（1，2）、N（2，1）都在反比例函数的图象上，
∴S△MCO=S△NOD，
∴S△OMN=S△MCO+S梯形CDMN-S△NOD=S梯形CDMN=
1
2
（1+2）×（2-1）=
3
2
．
故填：
3
2
．
点评：本题考查反比例函数系数k的几何意义，过双曲线上的任意一点分别向两条坐标轴作垂线，与坐标轴围成的矩形面积就等于|k|．本知识点是中考的重要考点，同学们应高度关注．
练习册系列答案
相关题目
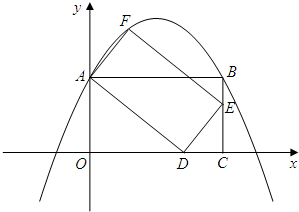精英家教网已知，平面直角坐标系上有A（a，0）、B（0，-b）、C（b，0）三点，且a≥b＞0，抛物线y=（x-2）（x-m）-（n-2）（n-m）． （m，n为常数，且m+2≥2n＞0），经过点A和点C，顶点为P
（1）当m，n满足什么关系时，S△AOB最大；
（3）如图，当△ACP为直角三角形时，判断以下命题是否正确：“直角三角形DEF的三个顶点都在这条抛物线上，且DF∥x轴，那么△ACP与△DEF斜边上的高相等”，如果正确请予以证明，不正确请举出反例．
如图，平面直角坐标系中，矩形ABCO的边OA在y正半轴上，OC在x正半轴上，点D是线段OC上一点，过点D作DE⊥AD交直线BC于点E，以A、D、E为顶点作矩形ADEF．
（1）求证：△AOD∽△DCE；
（2）若点A坐标为（0，4），点C坐标为（7，0）．
①当点D的坐标为（5，0）时，抛物线y=ax2+bx+c过A、F、B三点，求点F的坐标及a、b、c的值；
②若点D（k，0）是线段OC上任意一点，点F是否还在①中所求的抛物线上？如果在，请说明理由；如果不在，请举反例说明；
（3）若点A的坐标是（0，m），点C的坐标是（n，0），当点D在线段OC上运动时，是否也存在一条抛物线，使得点F都落在该抛物线上？若存在，请直接用含m精英家教网、n的代数式表示该抛物线；若不存在，请说明理由．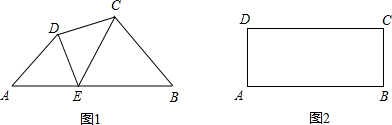
如图1，在四边形ABCD的AB边上任取一点E（点E不与点A、点B重合），分别连接ED、EC，可以把四边形ABCD分成3个三角形．如果其中有2个三角形相似，我们就把点E叫做四边形ABCD的AB边上的相似点；如果这3个三角形都相似，我们就把点E叫做四边形ABCD的AB边上的强相似点．
（1）若图1中，∠A=∠B=∠DEC=50°，说明点E是四边形ABCD的AB边上的相似点；
精英家教网
（2）①如图2，画出矩形ABCD的AB边上的一个强相似点．（要求：画图工具不限，不写画法，保留画图痕迹或有必要的说明．）
②对于任意的一个矩形，是否一定存在强相似点？如果一定存在，请说明理由；如果不一定存在，请举出反例．
（3）在梯形ABCD中，AD∥BC，AD＜BC，∠B=90°，点E是梯形ABCD的AB边上的一个强相似点，判断AE与BE的数量关系并说明理由．
（2010•同安区质检）如图，在直角梯形ABCD中，∠A=90°，DC∥AB，CD=
12
AB=a，AD=3，E为线段BC上的动点（不与点B、点C重合），EF⊥AB于F，EG⊥AD于G，设EF=x，EG=y．
（1）求y关于x的函数关系式（系数可含a），并写出自变量x的取值范围；
（2）无论a为何正数，在点E运动的过程中，我们都可以看出y随着x的增大而减小．小明说此时四边形AFEG的周长w也是随着x的增大而减小．你认为他说的是否正确？如果正确，请说明理由；如果不正确，请举出反例．
（1）如图1，矩形ABCD中，AB：BC=2：3，点E、F分别在边AD和CD上，且AF⊥BE于O，求
AF
BE
的值；
（2）在上面的问题中，若
AF
BE
=k，通过变式，我们可以得到如下的两个命题：
①若将AF沿直线AB方向平移到PQ，将BE沿直线AD方向平移到RS，然后将PQ与RS同时绕点O旋转（保持PQ与RS垂直），则
PQ
RS
=k；
②设P、R、Q、S依次是矩形的边AB、BC、CD、DA上的点，若=k，则PQ⊥RS．精英家教网
（Ⅰ）判断命题的真假性：①
 
；②
 
；（在横线上填“真命题”或“假命题”）
（Ⅱ）若其中有假命题，请你在图3中，用画图的方法举反例进行说明；若以上两个命题都是真命题，请选择其中一个给予证明．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网