题目内容
【题目】如图，在矩形
中，
，
.
（1）如果
、
分别是
、
的中点，
是对角线
上的点，
，则
的长为________；
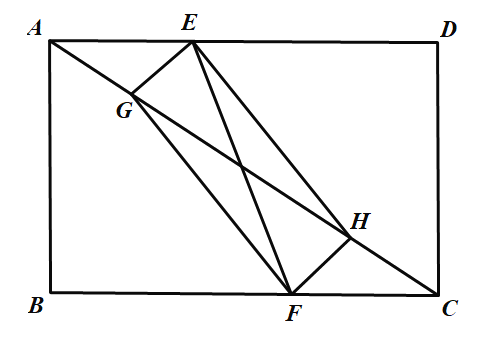
（2）如果、分别是、上的点，,
是对角线上的点.下列判断正确的是_____．
①在上存在无数组,，使得四边形
是平行四边形；
②在上存在无数组,，使得四边形是矩形；
③在上存在无数组,，使得四边形是菱形；
④当
时，存在、、，使得四边形是正方形.
【答案】2或8 ①②③④
【解析】
（1）分两种情况，点G在线段OA或OC上，首先利用矩形的性质证明
，得到
，然后利用直角三角形斜边中线的性质得出
，然后利用勾股定理求出AC的长度，进而可得到AO的长度，最后利用
即可求解．
（2）①利用平行四边形的判定方法判定即可；
②利用矩形的判定方法判定即可；
③利用菱形的判定方法判定即可；
④先假设存在这样的正方形，然后利用正方形的性质求出AE的长度，看是否能找到满足条件的E,F,H点，进而可得出结论．
（1）当点G在线段OC上时，如图，
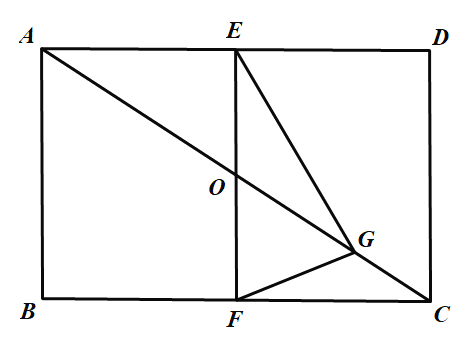
∵四边形ABCD是矩形，
∴
，
．
∵点E,F分别是AD,BC的中点，
∴
．
在
和
中，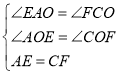
，
．
，
．
，
，
，
；
当点G在线段OA上时，如图，
同理可求
，
∴
，
综上所述，AG的长度为2或8；
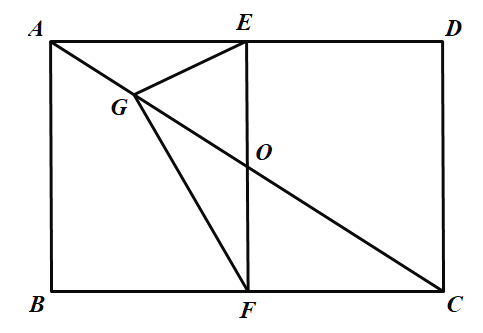
（2）只要满足
即可得出四边形
是平行四边形，故①正确
理由如下：
∵四边形ABCD是矩形，
∴
，
．
在
和
中，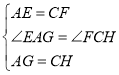
，
，
∴四边形是平行四边形；
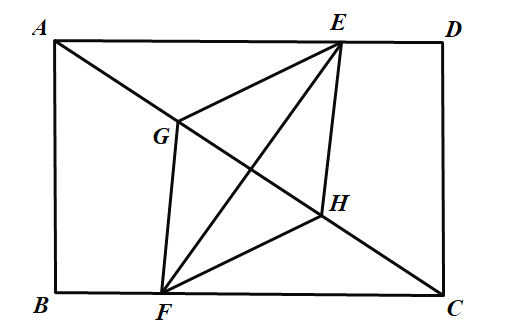
②在①的基础上再保证
即可证明四边形是矩形，而满足条件的有无数个，故②正确；
③在①的基础上，需要再满足
，这时E,F点的位置就固定下来了，但是只要满足
即可得到四边形是菱形，而满足条件的有无数个，故③正确；
④假设当
时，存在
、
、
，使得四边形是正方形，则有
，
，
，
．
，
，
．
，
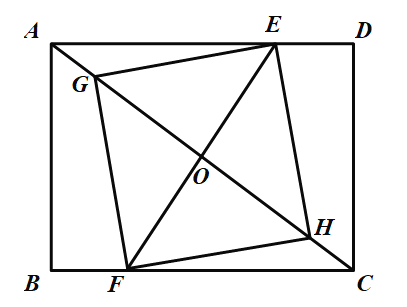
∴线段AD上存在点E，
∴只要同时满足
就能得到四边形是正方形，故④正确．
名校课堂系列答案
【题目】学完二次根式一章后，小易同学看到这样一题：“函数
中,自变量
的取值范围是什么？”这个问题很简单，根据二次根式的性质很容易得到自变量的取值范围.联想到一次函数，小易想进一步研究这个函数的图象和性质.以下是他的研究步骤：
第一步：函数中,自变量的取值范围是_____________.
第二步：根据自变量取值范围列表：
| -1 | 0 | 1 | 2 | 3 | 4 | |
| 0 | 1 |
|
| 2 |
|
__________.
第三步：描点画出函数图象.
在描点的时候，遇到了
，
这样的点，小易同学用所学勾股定理的知识，找到了画图方法，如图所示：
你能否从中得到启发，在下面的
轴上标出表示
、
、
的点，并画出的函数图象.
第四步：分析函数的性质.
请写出你发现的函数的性质(至少写两条)：
____________________________________________________________________________________________
____________________________________________________________________________________________
第五步：利用函数图象解含二次根式的方程和不等式.
（1）请在上面坐标系中画出
的图象，并估算方程
的解.
（2）不等式
的解是__________________.
