题目内容
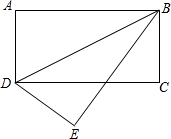 在如图的长方形纸片ABCD中,将△ABD沿BD折叠,点A落在点E处若∠ABD=35°,则∠CDE=
在如图的长方形纸片ABCD中,将△ABD沿BD折叠,点A落在点E处若∠ABD=35°,则∠CDE=20
20
°.分析:根据翻折变换的性质,∠ABD=∠DBE=35°,∠A=∠E=90°,可求出∠EBC的度数,又由于∠CDE=∠CBE,即求出答案.
解答:解:∵△BDE由△BDA折叠得到,
∴∠ADB=∠DBE,
∴∠ABD=∠DBE=35°,∠A=∠E=90°,
∴∠CDE=∠EBC=90°-∠ABD-∠DBE=90°-35°-35°=20°.
故答案为:20.
∴∠ADB=∠DBE,
∴∠ABD=∠DBE=35°,∠A=∠E=90°,
∴∠CDE=∠EBC=90°-∠ABD-∠DBE=90°-35°-35°=20°.
故答案为:20.
点评:本题考查了图形的翻折变换,解题过程中应注意折叠是一种对称变换,它属于轴对称,根据轴对称的性质,折叠前后图形的形状和大小不变,如本题中折叠前后角相等.

练习册系列答案
 口算心算速算应用题系列答案
口算心算速算应用题系列答案 同步拓展阅读系列答案
同步拓展阅读系列答案
相关题目
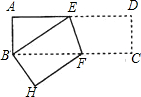 如图,长方形纸片ABCD中,AB=3cm,AD=9cm,将此长方形纸片折叠,使点D与点B重合,点C落在点H的位置,折痕为EF,则△ABE的面积为( )
如图,长方形纸片ABCD中,AB=3cm,AD=9cm,将此长方形纸片折叠,使点D与点B重合,点C落在点H的位置,折痕为EF,则△ABE的面积为( )| A、6cm2 | B、8cm2 | C、10cm2 | D、12cm2 |
 如图,长方形纸片ABCD中,BC=
如图,长方形纸片ABCD中,BC= 如图,长方形纸片OABC放入平面直角坐标系中,使OA、OC分别落在x轴、y)轴上,连结OB,将纸片OABC沿OB折叠,使点A落在点A′处,A′B与y轴交于点F,且知OA=1,AB=2.
如图,长方形纸片OABC放入平面直角坐标系中,使OA、OC分别落在x轴、y)轴上,连结OB,将纸片OABC沿OB折叠,使点A落在点A′处,A′B与y轴交于点F,且知OA=1,AB=2. 在如图的长方形纸片ABCD中,将△ABD沿BD折叠,点A落在点E处若∠ABD=35°,则∠CDE=________°.
在如图的长方形纸片ABCD中,将△ABD沿BD折叠,点A落在点E处若∠ABD=35°,则∠CDE=________°.