题目内容
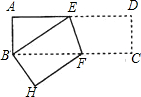如图，长方形纸片ABCD中，AB=3cm，AD=9cm，将此长方形纸片折叠，使点D与点B重合，点C落在点H的位置，折痕为EF，则△ABE的面积为（ ）| A、6cm2 | B、8cm2 | C、10cm2 | D、12cm2 |
分析：设AE=x，则ED=BE=9-x，根据勾股定理可求得AE，DE的长，从而不难求得△ABE的面积
解答：解：设AE=x，由折叠可知：ED=BE=9-x，
∵在Rt△ABE中，32+x2=（9-x）2
∴x=4，
∴S△ABE=
AE•AB=
×3×4=6（cm2）
故选A．
∵在Rt△ABE中，32+x2=（9-x）2
∴x=4，
∴S△ABE=
| 1 |
| 2 |
| 1 |
| 2 |
故选A．
点评：本题考查了利用勾股定理解直角三角形的能力．
练习册系列答案
相关题目
如图，长方形纸片ABCD中，AD=9，AB=3，将其折叠，使其点D与点B重合，点C至点C′，折痕为EF．求△BEF的面积？
23、如图，长方形纸片ABCD，沿折痕AE折叠边AD，使点D落在BC边上的点F处，已知AB=8，S△ABF=24，求EC的长．
如图，长方形纸片ABCD中，AD=BC=7，沿对称轴EF折叠，若折叠后A′B′与C′D′间的距离为6，则原纸片的宽AB=
如图，长方形纸片OABC放入平面直角坐标系中，使OA、OC分别落在x轴、y）轴上，连结OB，将纸片OABC沿OB折叠，使点A落在点A′处，A′B与y轴交于点F，且知OA=1，AB=2．