题目内容
 如图,长方形纸片OABC放入平面直角坐标系中,使OA、OC分别落在x轴、y)轴上,连结OB,将纸片OABC沿OB折叠,使点A落在点A′处,A′B与y轴交于点F,且知OA=1,AB=2.
如图,长方形纸片OABC放入平面直角坐标系中,使OA、OC分别落在x轴、y)轴上,连结OB,将纸片OABC沿OB折叠,使点A落在点A′处,A′B与y轴交于点F,且知OA=1,AB=2.(1)分别求出OF的长度和点A′坐标;
(2)设过点B的双曲线为y=
| k | x |
2
2
;(3)如果D为反比例函数在第一象限图象上的点,且D点的横坐标为2,在x轴上求一点P,使PB+PD最小.
分析:(1)由折叠的性质可得∠OBA=∠OBA′,再由AB∥OC可知∠OBA=∠COB,继而得出∠COB=∠OBA′,故FB=FO,设FB=FO=x,则A′F=2-x,在Rt△OA′F中,根据勾股定理可得出OF,A′F的长,过点A′作A′E垂直x轴于点E,易得△OA'E∽△OBA,利用对应边成比例,可得出A'E、OE,继而得出点A'的坐标.
(2)将点B的坐标代入y=
(x>0),可得出k的值;
(3)先求出点D的坐标,作点D关于x轴的对称点D',连接D'B,则D'B与x轴的交点即是点P的位置,求出D'B的长度,即可得出答案.
(2)将点B的坐标代入y=
| k |
| x |
(3)先求出点D的坐标,作点D关于x轴的对称点D',连接D'B,则D'B与x轴的交点即是点P的位置,求出D'B的长度,即可得出答案.
解答:解:(1)由折叠的性质得:∠OBA=∠OBA′,
∵AB∥OC,
∴∠OBA=∠COB,
∴∠OBA'=∠COB,
∴OF=BF,
设FB=FO=x,则A′F=2-x,
在Rt△OA′F中,A′O2+A′F2=OF2,即12+(2-x)2=x2,
解得:x=
,
故OF=
;
过点A′作A′E垂直x轴于点E,如图①所示:

易得△OA'E∽△OBA,
∴
=
=
=
,
∴OE=
,A′E=
,
故点A′的坐标为(-
,
).
(2)∵OA=1,AB=2,
∴点B的坐标为(1,2),
将点B(1,2)代入y=
(x>0),可得:k=2.
(3)点D的横坐标为x=2,代入y=
,可得y=1,
故点D的坐标为(2,1),
作点D关于x轴的对称点D',连接D'B,则D'B与x轴的交点即是点P的位置,如图②所示:

点D'(2,-1),
设直线BD'的解析式为:y=kx+b,
则
,
解得:
,
∴直线BD'的解析式为:y=-3x+5,
令y=0,可得x=
,
故点P的位置为(
,0),此时PB+PD最小,最小值=BD'=
=
.
即PB+PD的最小值为
.
∵AB∥OC,
∴∠OBA=∠COB,
∴∠OBA'=∠COB,
∴OF=BF,
设FB=FO=x,则A′F=2-x,
在Rt△OA′F中,A′O2+A′F2=OF2,即12+(2-x)2=x2,
解得:x=
| 5 |
| 4 |
故OF=
| 5 |
| 4 |
过点A′作A′E垂直x轴于点E,如图①所示:

易得△OA'E∽△OBA,
∴
| OE |
| OA |
| A′E |
| AB |
| OA′ |
| OB |
| 1 | ||
|
∴OE=
| ||
| 5 |
2
| ||
| 5 |
故点A′的坐标为(-
| ||
| 5 |
2
| ||
| 5 |
(2)∵OA=1,AB=2,
∴点B的坐标为(1,2),
将点B(1,2)代入y=
| k |
| x |
(3)点D的横坐标为x=2,代入y=
| 2 |
| x |
故点D的坐标为(2,1),
作点D关于x轴的对称点D',连接D'B,则D'B与x轴的交点即是点P的位置,如图②所示:

点D'(2,-1),
设直线BD'的解析式为:y=kx+b,
则
|
解得:
|
∴直线BD'的解析式为:y=-3x+5,
令y=0,可得x=
| 5 |
| 3 |
故点P的位置为(
| 5 |
| 3 |
| (2-1)2+(-1-1)2 |
| 5 |
即PB+PD的最小值为
| 5 |
点评:本题考查了反比例函数的综合,涉及了翻折变换、待定系数法求反比例函数解析式及轴对称求最短路径的知识,解答本题要求同学们具有扎实的基本功,注意数形结合思想的运用.

练习册系列答案
 导学教程高中新课标系列答案
导学教程高中新课标系列答案 小学课时特训系列答案
小学课时特训系列答案
相关题目
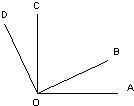

 如图,长方形纸片OABC放入平面直角坐标系中,使OA、OC分别落在x轴、y轴上,连结OB,将纸片OABC沿OB折叠,使点A落在点A′处,A′B与y轴交于点F,且知OA=1,AB=2.
如图,长方形纸片OABC放入平面直角坐标系中,使OA、OC分别落在x轴、y轴上,连结OB,将纸片OABC沿OB折叠,使点A落在点A′处,A′B与y轴交于点F,且知OA=1,AB=2. 如图,长方形纸片OABC放入平面直角坐标系中,使OA、OC分别落在x轴、y轴上,连结OB,将纸片OABC沿OB折叠,使点A落在点A′处,A′B与y轴交于点F,且知OA=1,AB=2.
如图,长方形纸片OABC放入平面直角坐标系中,使OA、OC分别落在x轴、y轴上,连结OB,将纸片OABC沿OB折叠,使点A落在点A′处,A′B与y轴交于点F,且知OA=1,AB=2. (x>0),则k=______;
(x>0),则k=______;