题目内容
设x为实数,定义[x]为不小于实数x的最小整数(如[π]=4,[-π]=-3),则关于实数x的方程[3x+1]=2x-
的全部实根之和等于 .
| 1 |
| 2 |
考点:取整计算
专题:
分析:设2x-
=k?Z,则x=
,3x+1=k+1+
,于是原方程等价于[
]=-1,从而可得k=-5或-4,求出相应的x,就可求出全部实根之和.
| 1 |
| 2 |
| 2k+1 |
| 4 |
| 2k+3 |
| 4 |
| 2k+3 |
| 4 |
解答:解:设2x-
=k?Z,则x=
,
3x+1=k+1+
,于是原方程等价于[
]=-1,
即-2<
≤-1,
从而-
<k≤-
,
解得:k=-5或-4,
相应的x的值为:-
,-
,
故全部实根之和等于:-4.
故答案为:-4.
| 1 |
| 2 |
| 2k+1 |
| 4 |
3x+1=k+1+
| 2k+3 |
| 4 |
| 2k+3 |
| 4 |
即-2<
| 2k+3 |
| 4 |
从而-
| 11 |
| 2 |
| 7 |
| 2 |
解得:k=-5或-4,
相应的x的值为:-
| 9 |
| 4 |
| 7 |
| 4 |
故全部实根之和等于:-4.
故答案为:-4.
点评:此题主要考查了取整计算,求出相应x的值是解题关键.

练习册系列答案
相关题目
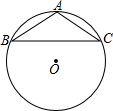 如图已知,AB=AC=6,BC=10,求半径r.
如图已知,AB=AC=6,BC=10,求半径r.