题目内容
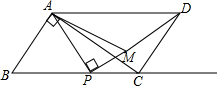 已知:平行四边形ABCD中,对角线AC⊥AB,AB=15,AC=20,点P为射线BC上一动点,AP⊥PM(点M与点B分别在直线AP的两侧),且∠PAM=∠CAD,连接MD.
已知:平行四边形ABCD中,对角线AC⊥AB,AB=15,AC=20,点P为射线BC上一动点,AP⊥PM(点M与点B分别在直线AP的两侧),且∠PAM=∠CAD,连接MD.(1)当点M在平行四边形内时,BP=x,AP=y,求解析式,并求定义域.
(2)图中是否存在与△AMD相似的三角形?请说明理由.
(3)当△AMD为等腰三角形时,求BP的长.
考点:相似形综合题,等腰三角形的判定与性质,勾股定理,平行四边形的性质,相似三角形的判定与性质
专题:压轴题,分类讨论
分析:(1)可先考虑临界位置(点M在边BC、DC上),从而得到自变量x的取值范围,然后过点A作AH⊥BC于H,如图3,在Rt△AHP中,运用勾股定理就可求出y与x的关系式.
(2)易证△APM∽△ACD,则有
=
.由∠PAM=∠CAD得∠PAC=∠MAD,就可得到△APC∽△AMD.
(3)由于△APC∽△AMD,因此可将△AMD为等腰三角形的问题转化为△APC为等腰三角形的问题,就可解决问题.
(2)易证△APM∽△ACD,则有
| AP |
| AC |
| AM |
| AD |
(3)由于△APC∽△AMD,因此可将△AMD为等腰三角形的问题转化为△APC为等腰三角形的问题,就可解决问题.
解答:解:(1)考虑两个临界位置:
①当点M在线段BC上时,如图1.

则∠APB=180°-∠APM=180°-90°=90°.
在RtABC中,
∵∠BAC=90°,AB=15,AC=20,
∴BC=
=25.
∵S△ABC=
AB•AC=
BC•AP,
∴AP=
=
=12.
在RtAPB中,
∵∠APB=90°,AB=15,AP=12,
∴BP=9.
②当点M在线段DC上时,此时点M与点D重合,点P与点C重合,如图2.

则BP=BC=25.
∴当点M在平行四边形内时,x的取值范围是9<x<25.
过点A作AH⊥BC于H,如图3.

则有AH=12,BH=9,在Rt△AHP中,
∵∠AHP=90°,AH=12,AP=y,PH=
,
∴122+(x-9)2=y2.
整理得:y2=x2-18x+225.
∵y>0,∴y=
.
∴y与x的关系式为y=
,定义域为9<x<25.
(2)存在与△AMD相似的三角形.
理由如下:
如图3,

∵四边形ABCD是平行四边形,
∴AD=BC=25,DC=AB=15,AB∥DC.
∴∠ACD=∠BAC=90°.
∴∠APM=∠ACD=90°.
∵∠PAM=∠CAD,
∴△APM∽△ACD.
∴
=
.
∵∠PAM=∠CAD,
∴∠PAC=∠MAD.
∴△APC∽△AMD.
(3)∵△APC∽△AMD,
∴
=
=
.
①若AM=AD,则AP=AC.
此时点P与点C重合,点M与点D重合,
△AMD不存在,故舍去.
②若MA=MD,则PA=PC,如图4.

∵PA=PC,
∴∠PAC=∠PCA.
∵∠BAC=90°,
∴∠BAP+∠PAC=90°,∠ABC+∠BCA=90°.
∴∠BAP=∠ABC.
∴PA=PB.
∴PB=PC.
∴PB=
BC=
.
③若DA=DM,则CA=CP.
Ⅰ.点P在线段BC上,如图5.

则CP=CA=20.
所以PB=BC-CP=25-20=5.
Ⅱ.点P在线段BC的延长线上,如图6.

则CP=CA=20.
所以PB=BC+CP=25+20=45.
综上所述:当△AMD为等腰三角形时,BP的长为
或5或45.
①当点M在线段BC上时,如图1.

则∠APB=180°-∠APM=180°-90°=90°.
在RtABC中,
∵∠BAC=90°,AB=15,AC=20,
∴BC=
| AB2+AC2 |
∵S△ABC=
| 1 |
| 2 |
| 1 |
| 2 |
∴AP=
| AB•AC |
| BC |
| 15×20 |
| 25 |
在RtAPB中,
∵∠APB=90°,AB=15,AP=12,
∴BP=9.
②当点M在线段DC上时,此时点M与点D重合,点P与点C重合,如图2.

则BP=BC=25.
∴当点M在平行四边形内时,x的取值范围是9<x<25.
过点A作AH⊥BC于H,如图3.

则有AH=12,BH=9,在Rt△AHP中,
∵∠AHP=90°,AH=12,AP=y,PH=
|
∴122+(x-9)2=y2.
整理得:y2=x2-18x+225.
∵y>0,∴y=
| x2-18x+225 |
∴y与x的关系式为y=
| x2-18x+225 |
(2)存在与△AMD相似的三角形.
理由如下:
如图3,

∵四边形ABCD是平行四边形,
∴AD=BC=25,DC=AB=15,AB∥DC.
∴∠ACD=∠BAC=90°.
∴∠APM=∠ACD=90°.
∵∠PAM=∠CAD,
∴△APM∽△ACD.
∴
| AP |
| AC |
| AM |
| AD |
∵∠PAM=∠CAD,
∴∠PAC=∠MAD.
∴△APC∽△AMD.
(3)∵△APC∽△AMD,
∴
| AP |
| AM |
| AC |
| AD |
| PC |
| MD |
①若AM=AD,则AP=AC.
此时点P与点C重合,点M与点D重合,
△AMD不存在,故舍去.
②若MA=MD,则PA=PC,如图4.

∵PA=PC,
∴∠PAC=∠PCA.
∵∠BAC=90°,
∴∠BAP+∠PAC=90°,∠ABC+∠BCA=90°.
∴∠BAP=∠ABC.
∴PA=PB.
∴PB=PC.
∴PB=
| 1 |
| 2 |
| 25 |
| 2 |
③若DA=DM,则CA=CP.
Ⅰ.点P在线段BC上,如图5.

则CP=CA=20.
所以PB=BC-CP=25-20=5.
Ⅱ.点P在线段BC的延长线上,如图6.

则CP=CA=20.
所以PB=BC+CP=25+20=45.
综上所述:当△AMD为等腰三角形时,BP的长为
| 25 |
| 2 |
点评:本题考查了相似三角形的判定与性质、等腰三角形的判定与性质、平行四边形的性质、勾股定理等知识,考查了分类讨论及转化的数学思想,有一定的综合性.

练习册系列答案
相关题目
 已知四边形ABCD中,AD=a,CD=b,AB=AC=BC=c,求BD的最大值.
已知四边形ABCD中,AD=a,CD=b,AB=AC=BC=c,求BD的最大值. 如图,OA=OB,OC=OD,∠AOC=∠BOD,求证:AB∥CD.
如图,OA=OB,OC=OD,∠AOC=∠BOD,求证:AB∥CD.