题目内容
12.若分式$\frac{{{x^2}-2x+1}}{x+1}$的值为正数,则x的取值范围是x>-1且x≠1.分析 分式$\frac{{{x^2}-2x+1}}{x+1}$的值是正数,则只需分子和分母同号,即同正或同负,再进一步解不等式组.
解答 解:因为分式$\frac{{{x^2}-2x+1}}{x+1}$的值为正数,
∴分式化简为:$\left\{\begin{array}{l}{{x}^{2}-2x+1>0}\\{x+1>0}\end{array}\right.$或$\left\{\begin{array}{l}{{x}^{2}-2x+1<0}\\{x+1<0}\end{array}\right.$,
因为x2-2x+1=(x-1)2≥0,所以$\left\{\begin{array}{l}{{x}^{2}-2x+1<0}\\{x+1<0}\end{array}\right.$不合题意,舍去,
解得不等式组$\left\{\begin{array}{l}{{x}^{2}-2x+1>0}\\{x+1>0}\end{array}\right.$:
可得:x>-1且x≠1,
故答案为:x>-1且x≠1.
点评 此题考查了根据分式的值的符号来判断分子和分母的符号,要求能够熟练解不等式组.

练习册系列答案
相关题目
3.在下面四个几何体中,俯视图是三角形的是( )


| A. | ① | B. | ② | C. | ③ | D. | ④ |
20.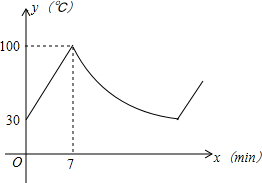 某品牌的饮水机接通电源就进入自动程序:开机加热到水温100℃,停止加热,水温开始下降,此时水温(℃)与开机后用时(min)成反比例关系,直至水温降至30℃,饮水机关机.饮水机关机后即刻自动开机,重复上述自动程序.若在水温为30℃时,接通电源后,水温y(℃)和时间x(min)的关系如图所示,水温从100℃降到35℃所用的时间是( )
某品牌的饮水机接通电源就进入自动程序:开机加热到水温100℃,停止加热,水温开始下降,此时水温(℃)与开机后用时(min)成反比例关系,直至水温降至30℃,饮水机关机.饮水机关机后即刻自动开机,重复上述自动程序.若在水温为30℃时,接通电源后,水温y(℃)和时间x(min)的关系如图所示,水温从100℃降到35℃所用的时间是( )
 某品牌的饮水机接通电源就进入自动程序:开机加热到水温100℃,停止加热,水温开始下降,此时水温(℃)与开机后用时(min)成反比例关系,直至水温降至30℃,饮水机关机.饮水机关机后即刻自动开机,重复上述自动程序.若在水温为30℃时,接通电源后,水温y(℃)和时间x(min)的关系如图所示,水温从100℃降到35℃所用的时间是( )
某品牌的饮水机接通电源就进入自动程序:开机加热到水温100℃,停止加热,水温开始下降,此时水温(℃)与开机后用时(min)成反比例关系,直至水温降至30℃,饮水机关机.饮水机关机后即刻自动开机,重复上述自动程序.若在水温为30℃时,接通电源后,水温y(℃)和时间x(min)的关系如图所示,水温从100℃降到35℃所用的时间是( )| A. | 27分钟 | B. | 20分钟 | C. | 13分钟 | D. | 7分钟 |
4.扇形的半径为30cm,圆心角为120°,此扇形的弧长是( )
| A. | 20πcm | B. | 10πcm | C. | 10cm | D. | 20cm |
1.下列各数中,比-1小的数是( )
| A. | -2 | B. | 0 | C. | 1 | D. | 2 |
2.4的算术平方根是( )
| A. | -2 | B. | ±2 | C. | 2 | D. | 16 |
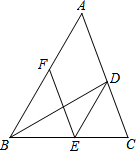 如图,BD是△ABC的角平分线,点E,F分别在BC,AB上,且DE∥AB,EF∥AC.
如图,BD是△ABC的角平分线,点E,F分别在BC,AB上,且DE∥AB,EF∥AC.