题目内容
12.已知一元二次方程x2-4x+m=0有唯一实数根,求($\frac{1}{m+2}$-$\frac{1}{m-2}$)÷$\frac{m}{{m}^{2}-4}$的值.分析 根据一元二次方程x2-4x+m=0有唯一实数根,求出m=4,然后将原式化简,代入求值即可.
解答 解:∵一元二次方程x2-4x+m=0有唯一实数根,
∴△=16-4m=0,
解得m=4,
原式=$\frac{1}{m+2}$×$\frac{(m-2)(m+2)}{m}$-$\frac{1}{m-2}$×$\frac{(m-2)(m+2)}{m}$
=$\frac{m-2}{m}$-$\frac{m+2}{m}$
=-$\frac{4}{m}$,
当m=4时,原式=-$\frac{4}{4}$=-1.
点评 本题考查了分式的化简求值、根的判别式,熟悉通分和因式分解是解题的关键.

练习册系列答案
相关题目
7.下列各式成立的是( )
| A. | 2<$\sqrt{7}$<3 | B. | (2+5)2=22+52 | C. | m(m+b)=m2+b | D. | 2$\sqrt{2}$-$\sqrt{2}$=2 |

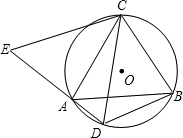 如图所示,△ABC是⊙O的内接三角形,AC=BC,D为⊙O中弧AB上一点,延长DA至点E,使CE=CD.
如图所示,△ABC是⊙O的内接三角形,AC=BC,D为⊙O中弧AB上一点,延长DA至点E,使CE=CD.